The scale insect (Icerya purchasi) is a major agricultural pest, especially for citrus growers. This pest arrived in the late 1800's from Australia and caused major devastation to the citrus crop in California, then spread to Florida. It was discovered that an Australian lady bug (Rodolia cardinalis, formerly Vedalia cardinalis) is a major predator of the scale insect, so orchard growers imported this predator in 1888 and 1889 and applied large numbers of these predators to their citrus groves to regulate the population of scale insects. In the late 1940's, the chemical industry demonstrated that application of DDT could effectively control the scale insect population, so orchard growers changed from controlling scale insects with lady bugs to chemical control with DDT. Unfortunately, DDT is not a discriminating insect control and kills both scale insects and their predators, the lady bugs. (Not to mention the other well-documented problems with this pesticide in the environment.)

The lady bug and scale insect populations form a Lotka-Volterra predator-prey relationship similar to the one studied in the lecture note section. If we let the scale insect population be defined by S(t) and the lady bug population be defined by L(t), then the predator prey dynamics of this population is governed by the system of differential equations:

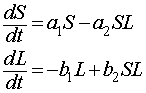
where a₁ is the growth rate of the scale insect, a₂ is the predation effect on scale insects, b₁ is the loss of lady bug population in the absence of prey, and b₂ is increase in lady bug population from predation on scale insects.

From our previous analysis, we find the equilibria for this predator-prey system by setting the derivatives equal to zero and solving for the equilibrium populations.

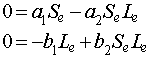
One of the equilibria is clearly the trivial equilibrium

(S_e, L_e) = (0, 0),

while the other equilibrium is readily solved giving

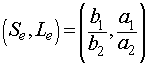
When DDT was introduced, this pesticide killed both the scale insect and the lady bug proportionally to their populations. In the mathematical model, this is very similar to the factor of netting fish we saw in the Volterra study. The Lotka-Volterra model for the scale insect and lady bug model can be written as

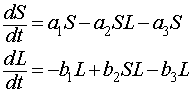
where a₃ is the loss of the scale insect due to DDT application and b₃ is the loss of lady bug population due to the pesticide. The magnitude of these parameters reflects the intensity of the application of the pesticide. The immediate effect of application of DDT is the sharp decline of all of the insects in the grove, which the agricultural industry desired. Thus, DDT was rapidly hailed as an easier way to improve production.

If we continue the equilibrium analysis of this model, we see that again there is the trivial equilibrium. (Thus, if the pesticide killed every scale insect, this pest would go extinct along with its predator.) The nonzero equilibrium can be readily seen to satisfy

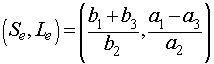
From this easy equilibrium analysis and the discussion of average populations over the limit cycle being equal to the equilibrium population, we see that application of DDT over the long term will result in more scale insects and fewer lady bugs, which is exactly the opposite of what the orchard growers want.

Conclusion: The application of pesticide over the longer term favors the pest species, which results in orchard growers applying more pesticide to control the pest species. This results in even more pests rebounding in the next few generations with fewer predators to control them. Thus, there is a never ending cycle of increasing pesticide dependence by the orchard growers. This process causes even larger amplitude oscillations, so nastier outbreaks. It follows that the farmers and public lose from pesticides, while the chemistry industry benefits! This analysis does not include the environmental harm caused by the pesticides, which in the case of DDT is well documented. Note that few pesticides undergo a rigorous analysis for their effect on humans and animals, so this problem will continue to persist for many years to come.