|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
San Diego State University -- This page last updated 30-Oct-01 |
Linear Differential Equations- Examples
|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
San Diego State University -- This page last updated 30-Oct-01 |
This section provides more worked examples to help learn how to analyze problems involving linear first order differential equations. The applications are to Arterial blood pressure, Malthusian growth of a population, Radioactive decay applied to ablation of the thyroid gland, Newton's Law of cooling, and pollution in a lake.
Example 1: Arterial Blood Pressure. In the lecture section, we determined the compliance and resistance for a normal healthy person. Now consider a trained athlete considered in very good condition. Suppose that this athlete has a pulse of 60 beats/min (at rest), a blood pressure of 120/75, and a measured cardiac output of 6 liters/min. Find the compliance, Ca , and systemic resistance, Rs of the arteries for this individual.
Solution: Recall that the compliance, Ca , was given by the formula
which we see is slightly larger than for a normal person. The systemic resistance, Rs, satisfies
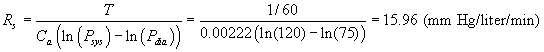
which we see is lower than for a normal person, which is what we would expect for someone in better condition.
Example 2: Malthusian Growth. Suppose that a culture of Escherichia coli is growing according to the Malthusian growth model
If the population doubles in 30 minutes, then find the value of r. If the initial population is 50,000, then find the population after 45 min and 2 hr.
Solution: If the initial population satisfies P(0) = P0, then the solution of the Malthusian growth model is given by
This population doubles when 2P0 = P0 e30r. Thus, e30r= 2 or 30r = ln(2) or r = ln(2)/30 = 0.0231 min-1.
With the initial condition P0 = 50,000, the solution can be written:
It follows that P(45) = 141,421 and P(120) = 800,000. Note that the second case follows easily from the fact that 2 hours is 4 doubling times or 24 = 16 times the initial population.
Example 3: Radioactive Decay and Hyperthyroidism.
Hyperthyroidism is a serious health problem caused by an overactive thyroid. The primary hormone released is thyroxine, which has a major stimulating effect on the release of other hormones in the endocrine system. In hyperthyroidism, the excess thyroxine causes the patient to release too many other hormones in the body, such as insulin and the sex hormones. The result can be low blood sugar causing lethargy or mood disorders and sexual dysfunction from too many sex hormones. One of the most common treatments for an over-active thyroid is to ablate the thyroid by giving a large dose of radioactive iodine, 131I. The 131I undergoes both b and g radioactive decays, which destroy tissue. The thyroid concentrates iodine brought into the body. The 131I, which is taken up by the thyroid, decays, and the energetic decays cause this gland to be destroyed. Afterwards the patient is given medicine to supplement the loss of thyroxine caused by this non-surgical procedure.
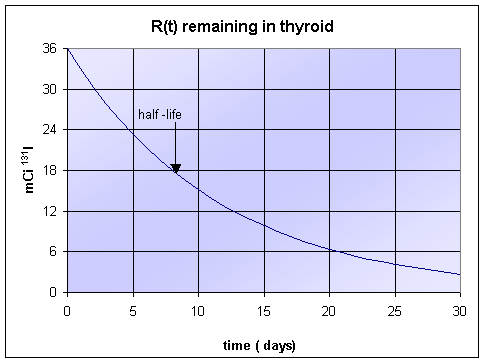
Based upon the thyroid condition and body mass, a standard dose for this procedure ranges from 110-150 mCi (milliCuries), which is given in a special "cocktail." It is assumed that almost 100% of the 131I is absorbed by the blood from the gut, then the thyroid uptakes 30% of this isotope of iodine, peaking around 3 days. (The remainder is excreted in the urine.) The half-life of 131I is 8 days, so this isotope fairly rapidly decays. Still the patient must remain in a designated room for 3-4 days for this procedure, so that he or she does not irradiate the public from his or her treatment.
Assume that a patient is given a 120 mCi cocktail of 131I and that 30% is absorbed by the thyroid. Find the amount of 131I in the thyroid (in mCi), if the patient is released four days after swallowing the radioactive cocktail. Calculate how many mCis the patient's thyroid retains after 30 days, assuming that it was taken up by the thyroid and not excreted in the urine.
Solution: It is assumed for simplicity of the model that the 131I is immediately absorbed into the thyroid, then stays there until it undergoes radioactive decay. Since the thyroid uptakes 30% of the 120 mCi, we will assume that the thyroid has 36 mCi immediately after the procedure. (Obviously, this is an oversimplification as it takes time for the 131I to accumulate in the thyroid.) However, it allows us to produce the simple model
The solution of this differential equation is
Since the half-life of 131I is 8 days, then we know that after 8 days there will be 18 mCi of 131I. Thus, we have
Thus, k = ln(2)/8 = 0.0866 day-1. At the time of the patient's release t = 4 days, so
After 30 days, we find
Example 4: Newton's Law of Cooling. We would like to determine whether a cup of tea cools more rapidly by adding cold milk right after brewing the tea or if you wait 5 minutes to add the milk. Assume that you begin with 4/5 cup of boiling hot tea, T(0) =100oC, and that the tea cools according to Newton's law of cooling
where Te = 20oC is the temperature of the room and k is a constant based on the properties of the cup and will be determined below.
a. In the first scenario, you let the tea cool for 5 minutes, then add 1/5 cup of cold milk, 5oC. Assume that after 2 minutes the tea has cooled to a temperature of 95oC, and determine the value of k (which we will assume holds throughout the solution of this problem). When you mix in the milk, assume that the temperature mixes perfectly in proportion to the volume of the two liquids. Find how long until the tea reaches a temperature of 70oC.
b. In the second case, you add 1/5 cup of cold milk, 5oC, immediately and mix it thoroughly, then allow the tea/milk mixture to cool to 70oC. Once again, find how long this takes.
Which situation gets your tea cooled the fastest?

Alice sighed wearily. `I think you might do something better with the time,' she said, `than waste it in asking riddles that have no answers.'
Lewis Carroll "Alice in Wonderland"
Solution: Begin by solving the initial value problem in a. in order to find the rate constant k. The information in the problem gives
As noted in the lecture notes, the easiest way to solve this differential equation is to make the substitution, z(t) = T(t) - 20, so z(0) =T(0) -20 =80. Since z'(t) = T '(t), the initial value problem above reduces to the following:
This has the solution
so T(t) = 80e-kt + 20.
From the condition, T(2) =95, we have
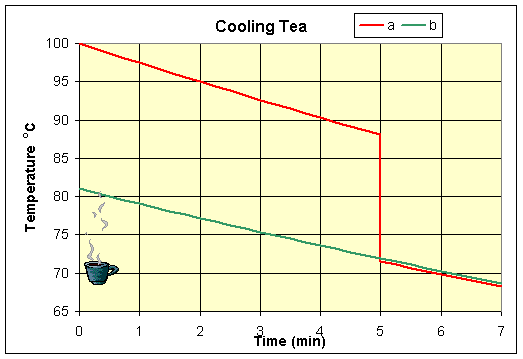
Thus, k = (ln(80/75))/2 = 0.03227. We substitute this value of k into the equation for T(t), then evaluate
We now mix the 4/5 cup of tea at 88.1oC with the 1/5 cup of milk at 5oC, which gives one cup of the tea/milk mixture at a temperature just following 5 minutes of
This results in the new initial value problem:
Following the procedure above with the same substitution, we have
This has the solution
so T(t) = 51.5e-k(t-5)+ 20. It is easy to check that this is the solution of the new initial value problem.
To find when the tea is 70oC, we must solve
Thus, k(t - 5) = ln(51.5/50), so t = 5 + (ln(51.5/50))/k = 5.92 min.
b. In this version of the problem, we begin with the mixing of the tea and milk to find the initial temperature for our computations. The mixing of 4/5 cup of tea at 100oC with 1/5 cup of milk at 5oC gives one cup of the tea/milk mixture at a temperature of
This results in the new initial value problem:
Using the same z(t) substitution, we have
This has the solution
so T(t) = 61e-kt+ 20.
To find when the tea is 70oC, we must solve
Thus, kt = ln(61/50), so t = (ln(61/50))/k = 6.16 min. It follows that by waiting to pour in the milk for 5 minutes, you save about 15 seconds in cooling time.
Example 5: Pollution in a Lake. Suppose that a new industry starts up river from a lake at t = 0 days, and this industry starts dumping a toxic pollutant, P(t), into the river at a rate of 7 g/day, which flows directly into the lake. The flow of the river is 1000 m3/day, which goes into the lake that maintains a constant volume of 400,000 m3. The lake is situated in a hot area and loses 50 m3/day of water to evaporation (pure water with no pollutant), while the remainder of the water exits at a rate of 950 m3/day through a river. We assume that all quantities are well-mixed and that there are no time delays for the pollutant reaching the lake from the river.
a. Write a differential equation that describes the concentration, c(t), of the pollutant in the lake, using units of mg/m3 (Note that 1000 mg = 1 g.), then solve the differential equation. If a concentration of only 2 mg/m3 is toxic to the fish population, then find how long until this level is reached. If unchecked by regulations, then find what the eventual concentration of the pollutant is in the lake, assuming constant output by the new industry.
b. Suppose that the lake is at this limiting level of pollutant and a new environmental law is passed that shuts down the industry at a new time t = 0 days. Write a new differential equation describing the situation following the shutdown of the industry and solve this equation. Calculate how long it takes for the lake to return to a level that allows fish to survive.
Solution: a. In this example we need to return to the original derivation of the lake pollution problem, where we used conservation of mass to balance the amounts of pollutant entering and leaving the lake. Recall that
If we let P(t) be the amount of pollutant in the lake at any time t, then the change in amount is given by P '(t). (The concentration is given by c(t) = P(t)/V and c'(t) = P '(t)/V.) The amount entering is the constant rate of pollutant dumped into the river, which is given by k = 7000 mg/day. The amount leaving is given by the concentration of the pollutant in the lake, c(t) (in mg/m3), times the flow of water out of the lake, f = 950 m3/day. Thus, we have the conservation of amount of pollutant given by the equation:
Note that the evaporation from the lake indirectly affects this amount equation by keeping the volume constant, but does not enter directly as no pollutant is assumed to leave from evaporation in the amount equation above. The concentration equation follows by dividing the equation above by the constant volume, V = 400,000 m3. Thus,
or
We can write this as
We make the change of variables, z(t) = c(t) - k/f, with z(0) = c(0) - k/f = -k/f, which gives the differential equation
This has the solution z(t) =-(k/f)e-f t/V = c(t) - k/f or
If a concentration of 2 mg/m3 is toxic to the fish population, then we want to find when c(t) = 2 mg/m3. Thus, we need to solve
t = ln(1.3726)/0.002375 ~ 133.3 days.
The limiting concentration has the exponential term go to zero. Thus, we have
b. The new environmental law shuts down the industry at a new time t = 0 days, so the equation above follows with k = 0 mg/day with c(0) = 7000/950 ~ 7.368 mg/m3. Thus, we need to solve
This has the solution
To find when the concentration is reduced to 2 mg/m3, we evaluate
t = ln(3.684)/0.002375 ~ 549 days.