|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 07-Oct-11 |
|
|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 07-Oct-11 |
|
The last section examined periodic phenomena and trigonometric functions. Trigonometric functions have been found to be useful in many other situations, particularly in approximating other complicated behavior. Joseph Fourier (1768-1830) discovered the use of series of trigonometric functions to approximate other phenomena, such as harmonic motion of vibrating strings. This section begins with a discussion of tidal flow, where the complicated flow of tides from the interaction of differing gravitational fields results in complex dynamics, which can be approximated by a short series of trigonometric functions with periods related to the astronomical bodies causing the tidal flow.
One of the great remaining frontiers that needs exploring on Earth is its oceans. Over half of the population on this planet lives within 100 miles of the oceans, so oceans play a significant role in human society. Tidal flow is part of the daily dynamics that affects the coastal zones. This is especially apparent in places like the Bay of Fundy in Nova Scotia, where the records show tides rising over 16 meters in a 6.25 hour time period.
Here in San Diego, the tidal flow is not so dramatic. However, the tides do affect a variety of marine behaviors. How are tides predicted and what is the basis for their variability? What causes the changes in amplitude and period between the high and low tides?
Most days there are two high tides (high-high and low-high) and two low tides (low-low and high-low). The primary forces generating the tides are from the gravity of the sun and the moon. These are complicated by the elliptical orbits of the moon around the Earth and the Earth around the sun and the influences of other planets. There are four dominant tidal forces for San Diego. The diurnal components (once per day) are denoted K1, the lunisolar force, and O1, the main lunar force, and the semidiurnal components (twice each day) are given by M2, the main lunar force, and S2, the main solar force. These forces are periodic with diurnal periods of approximately 24 hours and semidiurnal periods of 12 hours. However, there are variations from a 24 hour period as the periodic motion of the moon about the Earth must be considered. When the moon, Earth, and sun align at either a full moon or a new moon, then the tides are at their highest and lowest as the forces of gravity enhance tidal flow. The tides show the least variation when the moon is in its first or last quarter.
What mathematical tools can help predict the tides? One technique is to use a series of trigonometric functions to approximate the behavior of the tides. The standard programs, showing smooth tidal flow, usually use 12-14 trigonometric functions. Below we show graphs of the high and low tides for San Diego for the month of September 2002. In this case, the smooth curves are generated by using only four trigonometric functions from the four forces described above. The data points indicate the actual values of the high and low tides from standard tide tables. (Note that the actual date occurs on the graph at the end of each day, since we begin at t = 0.)
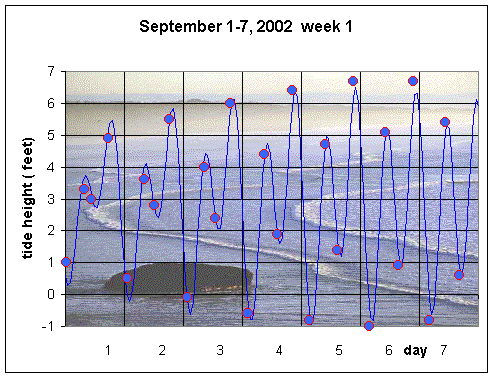
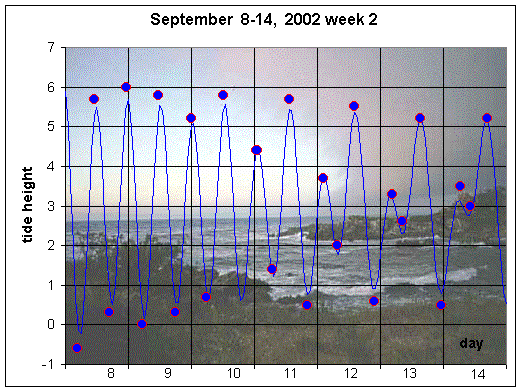
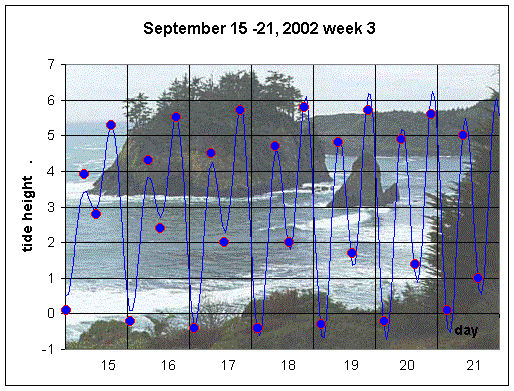
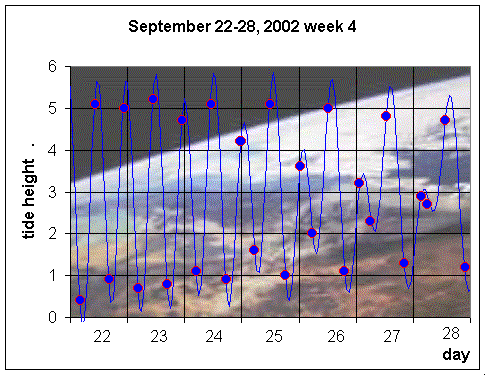
Let h(t) be the height of the tides in feet with t being the number of hours from midnight the first day of the month, then the h(t) used to generate the graphs above are formed by the sum of four cosine functions and a constant. The period of the cosine functions are designated by the periodic nature of the forces listed above. Recall that the diurnal forces are K1, the lunisolar force, and O1, the main lunar force, while the semidiurnal forces are M2, the main lunar force, and S2, the main solar force. There is a vertical shift of a0, then if the periods of the various forces are denoted by pi, the amplitudes are given by ai, and the phase shifts satisfy fi, i = 1,..,4. The periods are fixed based on the rotations of the moon and Earth, but the amplitudes of the forces and the phase lags of the tides are fit using a least squares best fit to the high and low tides for the month of September 2002. The specific form of h(t) is given by:
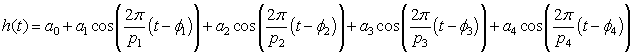
where the constants found by the least square best fit. As we did before, we chose the unique values with amplitude, ai > 0 and principle phase shift, 0 < fi < pi. The best fit to the vertical shift is a0 = 2.93733 ft. The other parameters are easily found from the table below.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
From this table, we see that the strongest force affecting the tides is the semidiurnal main lunar force. This shows that the moon has the greatest effect on the tides as you probably learned in high school science classes. The highest and lowest tides of the month coincide with the new moon and full moon. In the fall of 2002, the phases of the moon are given by
|
New Moon |
First Quarter |
Full Moon |
Last Quarter |
|
|
|
 |
|
|
August 8 |
August 15 |
August 22 |
August 30 |
|
September 6 |
September 13 |
September 21 |
September 29 |
|
October 6 |
October 12 |
October 20 |
October 28 |
|
November 4 |
November 11 |
November 19 |
November 26 |
For more information on the phases of the moon, you can examine lunar calendars. Note that if you are looking for these tides, the times on the calendars refer to Greenwich mean time, 8 hours ahead of San Diego.
We would like to determine exactly when the highest and lowest tides occur based on the mathematical model. (There will be an accompanying lab to have you work through similar calculations for the month of October 2000.) As we have seen before, the high and low points of a function are found by finding maxima and minima. Thus, we need to be able to differentiate our model, h(t). The high and low tides should occur when h'(t) = 0.
Differentiation of Trigonometric Functions -Sine and Cosine
We want to find the derivative of the sine and cosine functions. The derivative of these functions is found using the definition of the derivative and some trigonometric identities. The basic formulae for these derivatives are given by:
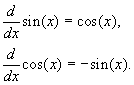
Geometrically, we recall that the derivative of a function is the value of the slope of the function at a given point. Below is an applet that shows a graph of the sine and cosine functions with overlaying graphs showing the values of the tangents to these functions. As you trace the curve of the sine (or cosine) function, then it is readily apparent that the slope of the tangent line follows the cosine (or negative of the sine) function. Click on the graph below, and track the function and its derivative through various angles.
More general rules of differentiation of these trigonometric functions require the use of the chain rule, much as we saw with either the exponential function or the logarithmic function. The general rules of differentiation for sine and cosine are given by the following. Assume that f(x) is a differentiable function, then
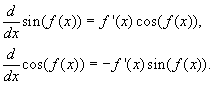
Example: Let f(x) = sin(x2 + 1). Find the derivative of f(x).
Solution: Since the derivative of x2 + 1 is 2x, the derivative of f(x) is
Example: Let f(x) = e-3xcos(x2 + 4). Find the derivative of f(x).
Solution: In this case, we need to apply the product rule. Thus, we see
For more examples, see the Worked Examples section.
As noted above, the highest and lowest tides of the month occur when the moon is in either the Full or New moon phases and the gravity of the moon assists the gravity of the sun to enlarge the tides. In September of 2002, there is a New moon on September 6. We would like to use the model to predict the highest high-high tide and lowest low-low tide for this week and determine the error between the model and the actual values for these tides. To find the times and heights of the high and low tides, we must locate extrema. Thus, we differentiate the function h(t), given by:
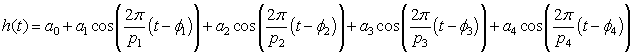
From the rules of differentiation above, the derivative of h(t) satisfies
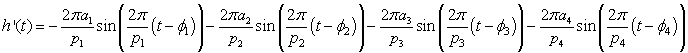
where the constants are given above. Clearly, this equation is too complicated to find the extrema by hand. However, the Computer labs have shown that finding zeroes of this function are readily done using either Excel's solver or Maples's fsolve. The mathematics behind these solving routines often uses a Newton's method, which is covered in a later section of these notes.
From the graphs above, we see that there are many local extrema for the month of September. In fact, there are usually four of them each day, so we must localize the search for the extrema using the visual information that we can gather from the graph. In the first week, when the new moon occurs, the data show that the highest tide is 6.7 feet on Sept. 6 , while the lowest tides are -1.0 feet on the same day. So what does our model using four cosine functions predict to be the highest and lowest tides of this week?
To calculate these values, we turn to Maple's fsolve routine. With the parameters from the table above substituted into the formula for h'(t), we set the derivative equal to zero. The lowest tide of the first week from the model is found to occur when t = 124.58 hours with a height of -0.86 feet. This corresponds to Sept. 6 at 4:35 am. The actual low-low tide on Sept. 6 is -1 feet occurring at 3:35 am, so the model overshoots the tide height by about 0.14feet and misses the time by 60 minutes. The highest tide of the first week as predicted by the model is found to be t = 142.56 hours with a height of 6.40 feet. This corresponds to Sept. 6 at 10:33 pm. The actual high-high tide happens at 9:36 pm at 6.7 feet. Thus, this prediction is similarly good, being off by only 0.3 feet in height and 57 minutes in time. Below we show the graph of the model for just Sept.6, including the data points of the high and low tides for that days.
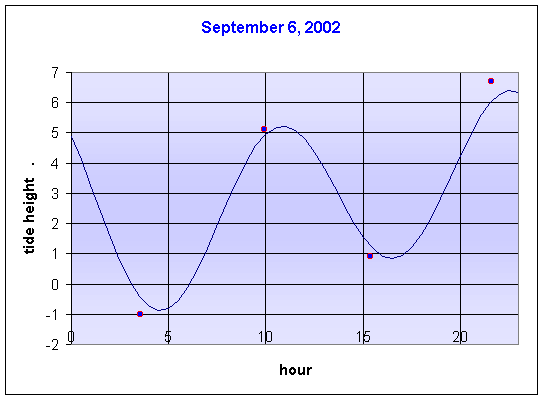
The calculations above show that our model introduces a moderate error, but then it only used four cosine functions to try to predict an entire month of high and low tides, so we see this is a reasonable approach to the problem. Obviously, the addition of more trigonometric function and more parameters can produce a much more accurate model, which is how the tides are actually predicted in the tide tables or when you call the information line (619-221-8824) for the San Diego Beach report.
This model was also run last year.