|
|
Math 122 - Calculus for
Biology II |
|
|---|---|---|
|
San Diego State University -- This page last updated 12-Nov-10 |
|
|
Math 122 - Calculus for
Biology II |
|
|---|---|---|
|
San Diego State University -- This page last updated 12-Nov-10 |
This section provides examples for indefinite integrals. These integrals naturally arise in time varying differential equations, which are illustrated below. Examples are provided for the flight of a ball under the influence of gravity and build up of toxins in a population of animals.
Below are a collection of indefinite integrals that illustrate how to take antiderivatives.
|
|
|
|
|
|
Solutions: Below we use the integration formulae developed in the lecture notes to solve the above integrals.
a. For polynomials, you increase the power of each term by one, then divide by the increased power. For exponentials of the form ekt, the integral divides the same exponential function by k. Thus, we have
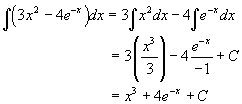
b. In this problem, the sine function goes to the negative of cosine, while the negative power is treated like terms of a polynomial by increasing the power by one. So the solution is given by
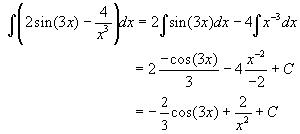
c. This integral has cosine going to sine and the antiderivative of the logarithm function.
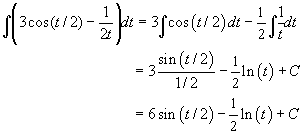
d. Here we change the square root to the 1/2 power, then just use the power rule for integration. The other terms follow the same rules as above.
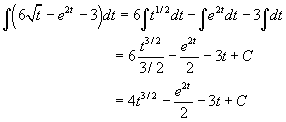
Below are several differential equations that illustrate the techniques we have learned to date. Not all of these require antiderivatives, but may instead require techniques from previous sections.
|
a. y ' = 4t - e-2t, y(0) = 10 |
b. y ' = 2t - sin(t), y(0) = 3 |
|
c. y ' = 4 - 2y, y(0) = 5 |
d. y ' = 4/t, y(1) = 2 |
Solutions: For any differential equation, you first identify the type of differential equation that you have. It is clear that a., b., and d. have only time varying functions on the right hand side of the differential equation, so these will be solved using integration. Example c above has a y on the right hand side, so we need to return to our earlier techniques for this problem.
a. We begin by finding the general solution. It satisfies
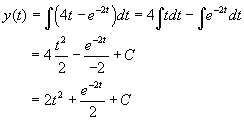
The initial condition gives y(0) = 10 = 1/2 + C, so C = 19/2. Thus, the solution to this inital value problem is
b. This problem starts like the last one with
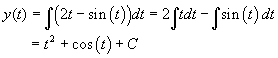
The initial condition gives y(0) = 3 = 1 + C or C = 2, so the solution to this inital value problem is
c. This problem is like the Newton law of cooling problems. We first see that
This suggests the substitution, z(t) = y(t) - 2. It follows that z(0) = y(0) - 2 = 3 and z' = y ', so we solve the initial value problem
This has the solution z(t) = 3e-2t= y(t) - 2. , which gives
d. This problem returns to using our integration techniques. The solution becomes
From the initial condition, y(1) = 2 = 4ln(1) + C, so C = 2. Thus, the solution is given by
A ball is thrown vertically with gravity (g = 32 ft/sec2) being the only force acting on the ball (air resistence is ignored). Assume that the ball begins at ground level, h(0) = 0 ft, and is given an initial upward velocity of 64 ft/sec (about 44 mph). Determine the height of the ball, h(t), at any time t > 0, and when the ball hits the ground. Find the maximum height of the ball and the velocity with which it hits the ground. Graph the solution for all time up until the ball hits the ground.
Solutions: Newton's law of motion says that mass times acceleration is equal to the sum of all the forces acting on the object. Thus, ma = -mg, where m is the mass of the ball, a is the acceleration of the ball, and -mg is the force of gravity (assuming up is positive). However, acceleration is the derivative of the velocity, and velocity is the derivative of position. The height of the ball, h(t), at any time t satisfies Newton's law of motion and is governed by the differential equation
The initial position is given by h(0) = 0, and the initial velocity is given by v(0) = h'(0) = 64 ft/sec.
We begin by solving the initial value problem for the velocity, which is only a first order differential equation. It is given by
We need to find a function whose derivative is -32, so the general solution to the differential equation is
where c is an arbitrary constant. Note that this is any straight line with a slope of -32. For the specific solution, we substitute the initial condition to obtain
Thus,
Now we need to solve the initial value problem
This is a problem of finding the antiderivative of 64 - 32 t. The general solution of this becomes
where again c is an arbitrary constant. Again we use the initial condition to give
Thus, the height of the ball at any time t for this problem is given by
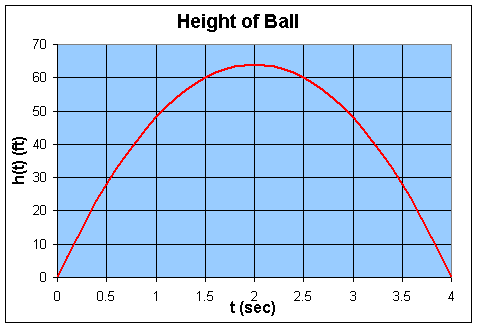
We can factor the equation above showing that h(t) = 16t(4 - t), which is zero when t = 0 or 4 sec. So the ball hits the ground 4 seconds after being tossed up. It follows that the velocity with which the ball hits the ground satisfies
The maximum height is when the velocity is zero, so solving v(t) = 64 - 32 t = 0, we have t = 2 sec. Evaluating h(2) = 64(2) -16(4) = 64 ft, it follows that the maximum height of the ball is 64 ft. Below is a graph of h(t) for 0 < t < 4.
For many years, lead (Pb) was an additive to paint used to reduce molds and improve adhesion. The federal govenment required leaded paint to be used in low income housing until the late 1960s. In the 1970s, it was discovered that, in inner cities, and in older houses everywhere, as leaded paint is shed or removed, it adds to the lead dust in and around homes, which can reach levels of 0.5% by weight of lead. The lead-laden dust has been found to be particularly problematic in the development of small children. They are exposed to lead from the dust ingested by normal hand-to-mouth play activities (crawling followed by thumb-sucking or playing with toys and sucking on them). The highest exposure to lead is for a relatively short time, but it comes at a critical time in neural development. The heavy metals do not leave the body and are often not discovered until after the child enters school at age 5 and is found to have neurological difficulties. This lead builds up in the children's bodies and has been linked to developmental problems with their nervous system. The long term effects of lead in a child can be severe. They include learning disabilities, decreased growth, hyperactivity, impaired hearing, and even brain damage. Scientists have discovered that lead concentrations as low as 10 mg/dl in the blood results in developmental toxicity. At 20 mg/dl in the blood, experiments show that nerve conduction slows. At levels over 40 mg/dl in the blood, Vitamin D metabolism and hemoglobin synthesis is impaired.
A model has been developed to determine the risks of children. This model (IEUBK - Integrated Exposure Uptake Biokinetic model) is designed to determine exposure from lead in air, water, soil, dust, diet and paint and other sources. Pharmacokinetic modeling is used to predict blood lead levels in children 6 months to 7 years of age. The four main components of the IEUBK model are: 1) an exposure model that relates environmental lead concentrations to age-dependent intake of lead into the gastrointestinal tract; 2) an absorption model that relates lead intake into the gastrointestinal tract and lead uptake into the blood; 3) a biokinetic model that relates lead uptake in the blood to the concentrations of lead in several organ and tissue compartments; and 4) a model for uncertainty in exposure and for population variability in absorption and biokinetics.
If we assume that the majority of the lead enters through the ingestion of contaminated dirt, then the amount of lead ingested depends on the hand-to-mouth activity of the child. This activity usually increases from birth to age 2 years, then rapidly declines as other forms of activity replace the hand-to-mouth activities. This allows a simpler model, which is similar to the model for mercury build up in fish.
a. Assume that the hand-to-mouth activity of a small girl in the age 0-24 months satisfies the differential equation
where a(t) is the activity time in hours per day and t is the age in months. Solve this differential equation and graph the solution. Determine the activity level in hours per day at age 24 months.
b. As noted above, the lead will enter the girl's body proportional to her activity time. Bioavailable lead is typically 0.1% of household dust by weight. That means that the total amount of lead (P(t)) in her body will satisfy the following differential equation:
where a(t) is the solution obtained from Part a. and k = 200 micrograms-day/hour of play/month. Find the solution P(t) and graph this solution.
c. Assume that this lead is uniformly distributed throughout the body. Find the lead level measured from blood samples at ages one and two. Typical measurements are in terms of micrograms/deciliter (mg/dl). Note that 10 dl of blood weighs about 1 kg, and a girl at age one (12 months) weighs 10 kg, while she weighs about 12 kg at age 2 (24 months).
Solution: a. The differential equation describing the activity of a child, a(t), is very similar to our study of Newton's law of cooling. Thus, we make the substitution z(t) = a(t) -12, with z'(t) = a'(t), so
which has the solution
Thus,
Below is a graph estimating the time of activity for a baby at ages from 0 to 24 months.
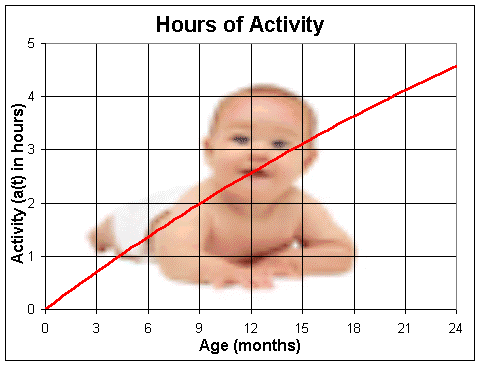
We see that a(24) = 12 (1-e-0.48) = 4.57, so at 24 months, the child spends about 4.6 hours or 4 hours and 35 minutes, in hand-to-mouth play.
b. The amount of lead accumulating in the baby girl's system satisfies the differential equation
since we are assuming that the lead is not leaving the body. Integration of this differential equation gives the solution. Recall that integration is representative of the accumulation or sum of the past lead acquired through the playing activity. It follows that
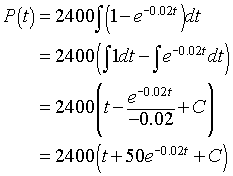
From the initial condition, P(0) = 2400((0) + 50 + C) = 0 or C = -50. It follows that the solution is given by
where P(t) is measured in mg accumulated by t months. A graph of this solution is given by
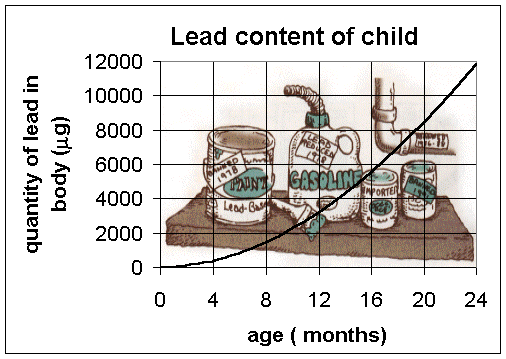
c. From our function for the amount of lead in a girl at age one (12 months) we have
Since the girl weighs 10 kg, the concentration is given by
c(12) = 3195 mg/10 kg = 31.95 mg/dl.
This value is clearly dangerous to neural development. (The actual lead tests are not very accurate with only an accuracy of +10mg/dl, but this is still within that reading frame.)
A similar calculation for a girl at age two or 24 months gives
Since the girl weighs 12 kg, the concentration is given by
c(24) = 11,854 mg/12 kg = 100.5 mg/dl.
This is a level which is considered deadly.