Computer Lab Help 10

This page is designed to provide helpful information about the laboratory questions. You will find more details in the Lab Manual that accompanies this course. Begin this lab and every lab by introducing yourself to your partner. Determine the times when you can meet together during the week before the lab is due at your next Lab session. You should start this lab and each lab by typing the name of each team member and your computer number on the Lab Cover Page (or a copy of it).

The first WeBWorK problem asks questions about this help page and appropriate lecture material. This should help you work through the Lab more smoothly. The first question examines three population growth models compared to data for a saw-tooth grain beetle population. You will be fitting functions and graphing them using techniques from the lab and class. Also, you will find equilibria and determine their stability. Finally, you will simulate the discrete dynamical models and fit them to beetle data. The second problem examines three models for the population growth of gregarious birds, including the Discrete Logistic Growth model, the Discrete Logistic Growth model with emigration, and a Cubic model that demonstrates the Allee effect. The last problem introduces you to a simple differential equation for the density of air at different elevations.

Problem 1: This is another problem using real data. The first part of this problem has you finding a discrete logistic growth model for these beetles based on the data. The problem has you rearrange the data in a way that allows you to find the best fitting updating function for the Discrete Dynamical model. Follow the directions carefully to obtain the right alignment of the data to use Excel's trendline polynomial fit and to get the right quadratic function here. Note that the function you are producing here is the updating function for finding the next population after two weeks have passed. The second part of Part a has you finding equilibria and determining the stability of the equilibria with derivatives. This part is probably best done using Maple. (You can probably do the logistic model by hand, but the other models will be much easier using Maple.) The next 3 parts of this question have you using Excel's Solver, much like you did in previous labs to find the best fitting updating functions for the models, then you will answer the same questions that you did for Part a. In Part e, you exercise your graphing skills that are important on tests. Again this will be made easier if you use Maple to help you accurately find derivatives and second derivatives to find critical points and points of inflection. Part e also asks you to step back and compare the different models. Try to get an overview of what you accomplished in this lab on the updating functions.

The last two parts have you simulate the models to compare the models to the time series data (the type most usually found). You take the original data (t in weeks and populations), then simulate each of the 4 models using the best updating functions that you found in the first part of the problem. (Simulation of these models is like the other simulations you have done in previous labs using dscrete dynamical models.) You set the initial condition to agree with the actual data at t = 0. Use Excel's Solver to minimize the sum of square errors between the data and the model simulation by changing only the initial value. The rest of the problem is just extracting information and writing a discussion.

Problem 2: This study begins with a set of data for the population dynamics of some birds, a time series. This is the usual manner of presenting data. However, the discrete dynamical models that we study use an updating function. In this problem you should work with one spreadsheet that creates the updating function, then later use another spreadsheet (or different location on the same spreadsheet) to analyze the time series.

To begin we concentrate on fitting the updating function to the data. Follow the directions carefully to obtain the right alignment of the population data (only) to use Excel's trendline polynomial fit and to get the right quadratic function here. Note that the function you are producing here is the updating function (Logistic Growth or quadratic function) for finding the next population, and you are NOT using the time data for this part of the problem. This portion of the problem has you graphing Pn+1 vs Pn.

On a separate spreadsheet (or different part of the one where you created the Updating function), make two columns with the original time series. Next to these two columns create a column for the model, which uses the best fitting updating function you found above. Create named variable, P0, that you use to begin your simulation of the logistic growth model (using the updating function). Starting the model with P0, use the updating function to simulate the population growth in the cell below. Find the sum of square errors between the data and this model simulation. With Excel's Solver, you adjust only the initial population to find the best fit of the model to the time series data.

In the next part of the question, you use your techniques from class (possibly with the help of Maple) to find the equilibria of the model and determine the local behavior of the model near those equilibria (Stable or Unstable, Monotonic or Oscillatory). This part returns you to understanding the importance of the graph of the updating function.

After working through the Logistic Growth model, you examine two alternative models. First you consider the system not being closed and consider the possibility of constant emigration on the dynamical model. The second alternative is fitting a cubic equation for a closed model, so passing through the origin. Both of these models have one additional parameter, so should fit the data better than the logistic growth model. You use Excel to find the polynomial fits, then use Excel's Solver to fit the best initial condition. You will also use the techniques learned in class for finding equilibria and studying the local behavior near those equilibria. 

The techniques employed to solve this question are similar to the ones that you have used before. The updating function simply uses the polynomial fit under Trendline in Excel (order 2 or 3). Be sure to format your model formula to have enough significant figures (preferably using the scientific notation option). The fitting of the time series is done by defining P0 on the spreadsheet, then entering P0 as the first element of the model simulation. The discrete dynamical model is simulated by filling down the model column using the updating function fit by Trendline. Another column in the spreadsheet is used to compute the square error between the time series data and the model. Excel's Solver is used to find the least sum of square errors (minimum) by changing only P0.

Problem 3: This lab examines a yeast culture that begins in exponential growth phase and continues until reaching stationary growth. We use Excel to determine the growth parameters for logistic growth of the yeast culture, identifying several of the key elements of this growth curve with techniques from Calculus and others that have been learned during this course.

You begin the problem by copying the data from the lab to an Excel spreadsheet. Place a label t in Cell A1 and label p in Cell B1. Put the Time data in Column A and Volume data (population) in Column B. These data are graphed (as data points) to see the growth of the culture. In Column C we want to put our logistic growth model given by the formula

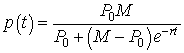
We make initial guesses at the growth parameters. Begin with a label P₀ in G1, then guess an initial value (1) in H1, then label G2 as M and put the largest value observed for the volume in the data and place this in H2. Label G3 as r, then as a rough guess, take r = 0.1 and place this in H3. We name these variables, then in Column D, you compute the square error between the model and the data (= (C2-B2)^2).  To find the least sum of square errors, we use Excel's Solver. You should see the sum of square errors drop and the values for P₀, M, and r change. This gives you your best model through the data.

The last step for Part a is to graph the model. In Column I, you put time, t, for the model (starting with t = 0), while Column J will have the equation for the model using the parameters in G1:G3 and the time from Column I. You increment the time to make sure that your graph has about 30-60 data points evenly spaced. (For example, if your data goes to 35 hours, then you might increment by one hour, so if I2 has t = 0, then take I3 to have = I2+1.) Fill down in Column J, then add this model to your graph.

Parts b and c follow from the techniques you have learned in class and Lab. You may want to use Maple to help with the differentiation. Make your plots using Excel.