This lab reviews the lecture material from the Linear Discrete Dynamical Models section and starts with the intuition behind the derivative, reviewing our allometric models. This lab begins by geometrically examining the relationship of the derivative to the slope of a tangent line, then uses the definition of the derivative to find the derivative of a couple of functions. The second part of this question has you use Maple to find the derivative. The second problem extends our population growth studies to a model with immigration and the logistic grrowth model. This question reviews the use of Solver to fit these models to population data. The third lab problem examines the growth of children, which introduces the derivative as a growth function. This lab has you reproducing similar results to the ones in the lecture notes, so you need to understand the material in the lecture notes to work this lab.

Problem 1: The first part of this question has you find two points on the curve generated by your function f(x) with the difference in the x values getting closer together. Create a table in Excel with Column A containing the values of x on the interval specified in your lab and separated by 0.05. (That is take the initial value of the interval and put it in cell A1, then let cell A2 have " = A1 + 0.05" in it and fill down to the final value in your interval.) This partitions your curve into enough points to get a smooth curve. In Column B, you enter your function. Compute the slopes of your different lines, then find the equations for each of your lines. Put your lines in Columns C-F, then graph all the values in Columns A-F to get the desired curves.

Computing the slope of the tangent line can be a tedious computation with lots of algebra. Maple does algebra and differentiation extremely well, so the next part of this lab problem uses Maple's symbolic algebra ability to handle the tedious computations. In class, we are finding the slope of the tangent line at a point (x₀, f(x₀)) by looking at the secant line through the points (x₀, f(x₀)) and (x₀ + h , f(x₀ + h)), then letting h tend to zero.

Below is an example that we will go through in lab to help you see the Maple commands for Parts b and c of Problem 1. As an example, let us consider the function

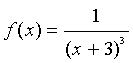
Suppose we want to find the slope of the secant line through the points (-2, f(-2)) = (-2, 1) and (-2 +h, f(-2 +h)) = (-2+h, 1/(1+h)³). (Note that you will be using a value different from x₀= -2, so make the appropriate changes below.) Below is the sequence of Maple commands to find the slope of both the secant and tangent lines.

First, you enter the function in the standard way for Maple:

> f : = x -> 1/(x+3)^3;

The slope of the secant line is found by the following:

> (f(-2+h) - f(-2))/h;
simplify(%);

The simplify command lets Maple find the easiest form of the expression that it chooses. (This may or may not be the best form to analyze.) Next we want the slope of the tangent line, which is found by letting h tend to zero. This is the derivative of f(x) at x = -2.

> m := limit(%, h = 0);

The m := is simply used to define the slope for future use. Maple has the limit command to take limits, which is mathematically a very difficult process. The % in Maple means to take the previous expression and place in the position with the %. (This can be a dangerous command to use, as it works on whatever you just did, not necessarily from the line above. If you do anything else, then use the cursor to return to a line with the %, then you may get the wrong result.)

Next we define tangent line (the command tline(x); gives you the equation of the tangent line), then plot both the function and the tangent line. (You will need to adjust the x and y values in the plot command to get the desired graph for your problem.)

> tline := x -> m*(x - (-2)) + f(-2); tline(x);

> plot({f(x), tline(x)}, x = -3..1, y = -10..20);

This completes Maple needed for the first parts of the problem.

The last part of the problem shows you how easily you can get a derivative using Maple. This is the way that many mathematicians actually do research when they need to accurately differentiate complicated expressions. Biologists often learn about a process through experimentation and recognizing patterns. Maple provides a powerful tool for performing differentiation, so it can act as your experimental device. Let Maple do the differentiations for you, then see if you can recognize patterns that eventually will become rules of differentiation.

You enter your function, for example:

> f := x -> x^2*exp(-1/x);

To differentiate, you simply type

> diff(f(x),x);

This is all that you have to do. Now that you have learned this basic Maple, you can use it to help you with answers to your differentiations in Homeworks. 

Problem 2: This problem is another examination of census data for some country. Part a is very similar to problems you have done before with simple Malthusian growth. Rather than actually using the solution of the discrete Malthusian growth model, you simulate the model with your named parameters for growth rate, r, and initial population, P₀. You use Excel's Solver to find the best fitting (least sum of square errors) parameters growth rate, r, and initial population, P₀. In Part b, the discrete Malthusian growth model adds a term for immigration, m. Once again, you name the 3 parameters in this model (use unique names with initial guesses suggested in the question), then simulate the discrete linear model of population growth with immigration. You should find Excel very good at simulating the model by entering the equation in the line below the initial population and filling down. Again, you use Excel's Solver to find the best fitting parameters for this model by letting it compute the least sum of square errors. The third model in this question uses a logistic growth model to simulate the census data. This is performed just like the immigration model, but uses the logistic growth equation given in your Lab question with its 3 parameters (with reasonable initial guesses for the parameters). Again Excel's Solver will find the parameters for this model that give you the least sum of square errors. If you want to be safe with your answer from Solver, then run Solver twice. The second run should leave an answer that is very close to your first execution of Solver.

The last part of the question with the logistic growth model asks for equilibria. These are found by substituting P_e for P_n and P_n+1 in the logistic growth equation, then solving for P_e. Since this is a quadratic equation, it should be easy for you to find the equilibria. One of the equilibria should be obvious from what you know should be true of population models.

Problem 3: This problem is meant to help motivate the idea of a derivative, which we will be studying over most of the rest of this course. The first part of this problem gives you more experience with allometric modeling using heights and weights of children. The remainder of the problem is designed to build intuition on the rate of gain of height or weight, which is a derivative. The lecture notes have details on computing the average rate of change in height, and this lab problem repeats a very similar calculation and adds the calculations for the average rate of gain of weight.