Problem 1: This problem extends the work that we are doing in class on finding minima and maxima of a function to a more complicated function. You will also find points of inflection. You will want to use Maple to differentiate this function and find values of the extrema. Maple will help to find the points of inflection by taking the second derivative. The Maple commands that you need are listed below (and you may want to review previous help sheets). First, define the function.

> f : = x -> (16-x^2)*exp(-x^2);

Next you should plot the function on the intervals listed to have an idea of what you are examining.

> plot(f(x), x = -10..10);

To find the derivative you type:

> df := diff(f(x), x);

You can simplify the expression by typing either of the following commands.

> simplify(%); factor(%);

To graph the derivative you type

> plot(df, x = -10..10);

To find when the derivative is zero, you first look on the graph to get an approximate idea. Then you type

> xc := fsolve(df = 0, x = 1..10); f(xc);

This second command gives the function value of the maximum or minimum.To find a point of inflection we take the second derivative, simplify it, then set it equal to zero. Finally, we do a function evaluation at the point of inflection.

> sdf := diff(df, x); factor(%);

> xpoi := fsolve(sdf = 0, x = 1..10); f(xpoi);

Problem 2: This problem is very similar to the material in the lecture notes, where we fit data to find the length of a fish as a function of its age using von Bertalanffy's equation. Also, we create an allometric model for the weight of a fish as a function of its length. The questions that you answer are very similar to the ones in Problem 13 in the homework problems. The fit to the von Bertalanffy equation is done very much the same way as you do the first question in this lab, while the fitting to the allometric model follows the techniques learned in Math 121 using Excel's trendline. This is readily accessed by right clicking on the data. You may need to increase the number of significant digits given to you by trendline. To obtain 5 significant figures, we right click on the formula, selecting Format Trendline Label, choose Number and Scientific, and finally select 5 Decimal Places. As in the first problem, the use of Maple might be valuable for helping with the differentiations (though you can practice your skills by doing them by hand). For this problem, the first and second derivatives are zero at t = 0, because the curve is very flat there. To get the point of inflection and the value of the function and the derivative at the point of inflection you need the following commands (assuming you see the point of inflection is between t = 1 and t = 20:

> p := t -> model goes here;

> dp := diff(p(t),t); # This gives the derivative

> sdp := diff(dp,t); # This gives the second derivative

> tp := fsolve(sdp=0, t = 1..20); # This gives the point of inflection

> p(tp); evalf(%); # This gives the population at the point of inflection

> subs(t = tp, dp); # This gives the derivative at the point of inflection

Problem 3: This lab examines a yeast culture that begins in exponential growth phase and continues until reaching stationary growth. We use Excel to determine the growth parameters for logistic growth of the yeast culture, identifying several of the key elements of this growth curve with techniques from Calculus and others that have been learned during this course.

You begin the problem by copying the data from the lab to an Excel spreadsheet. Place a label t in Cell A1 and label p in Cell B1. Put the Time data in Column A and Volume data (population) in Column B. These data are graphed (as data points) to see the growth of the culture. In Column C we want to put our logistic growth model given by the formula

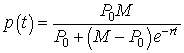
We make initial guesses at the growth parameters. Begin with a label P₀ in G1, then guess an initial value (1) in H1, then label G2 as M and put the largest value observed for the volume in the data and place this in H2. Label G3 as r, then as a rough guess, take r = 0.1 and place this in H3. We name these variables, then in Column D, you compute the square error between the model and the data (= (C2-B2)^2).  To find the least sum of square errors, we use Excel's Solver. You should see the sum of square errors drop and the values for P₀, M, and r change. This gives you your best model through the data.

The last step for Part a is to graph the model. In Column I, you put time, t, for the model (starting with t = 0), while Column J will have the equation for the model using the parameters in G1:G3 and the time from Column I. You increment the time to make sure that your graph has about 30-60 data points evenly spaced. (For example, if your data goes to 35 hours, then you might increment by one hour, so if I2 has t = 0, then take I3 to have = I2+1.) Fill down in Column J, then add this model to your graph.

Parts b and c follow from the techniques you have learned in class and Lab. You may want to use Maple to help with the differentiation. Make your plots using Excel.