Math 121 - Calculus for Biology I Spring Semester, 2004 Velocity and Tangent Lines - Examples
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 30-Dec-03

1. Flight of a Ball
2. Climbing a Salmon Ladder
3. Sequence of Secant Lines
4. Secant Line with h
5. Another Secant Line with h

The first example again examines the average velocity of a ball falling under gravity. The average velocity is the slope of the secant line for the height function. The geometric interpretation of the derivative of a function f(x) is the slope of the line tangent to the curve f(x) at some point. One means of finding the tangent line is to examine a sequence of secant lines, where the points on the curve are taken closer and closer together.

Example 1 (Flight of a Ball): A ball, which is thrown vertically with an initial velocity of 80 ft/sec and only the acceleration of gravity acting on the ball, satisfies the equation:

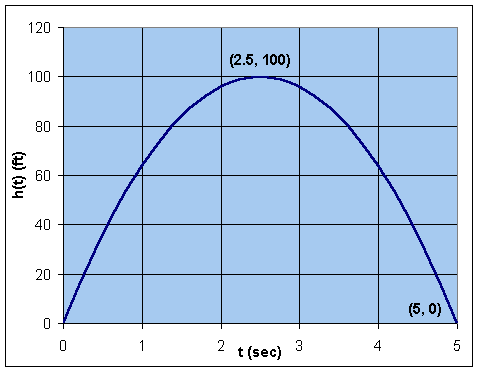
a. Sketch a graph of the height of the ball (in feet), h(t), showing clearly the maximum height and when the ball hits the ground.

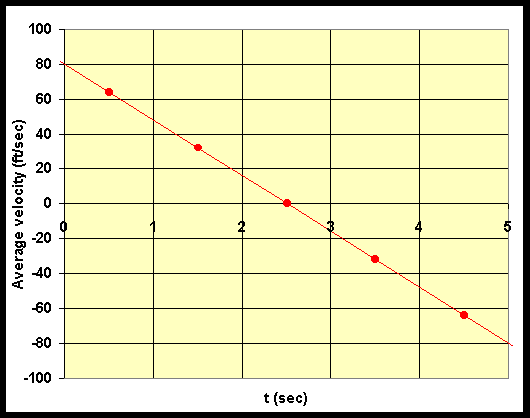
b. Find the average velocity of the ball between t = 0 and t = 1 and associate this velocity with t = 0.5. Repeat this process for each second of the flight of the ball, then sketch a graph of the average velocity as a function of time, t.

Solution: a. The graph of h(t) is a parabola with t-intercepts at t = 0 and t = 5, the latter being when the ball hits the ground. The vertex or maximum height of the ball occurs at the midpoint between these intercepts or t = 2.5 with h(2.5) = 100 ft. Below is a graph showing the height of the ball as a function of t.

 

b. The average velocity for the ball between t = 0 and t = 1 sec is given by

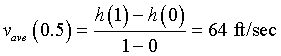
Similarly, the average velocities are computed between each pair of seconds from t = 0 to t = 5, and the results are summarized in the table below.

The graph of the average velocity is seen below and is a straight line. Note that the average velocity is zero at the maximum of the height curve, h(t).

 

Example 2(Leaping Salmon): A river is dammed, and a salmon ladder is built to enable the salmon to bypass the dam and continue to travel upstream to spawn. The vertical walls on the salmon ladder are 6 feet high. The salmon has to leap vertically upwards over the wall. The height of the salmon during its leap is given by

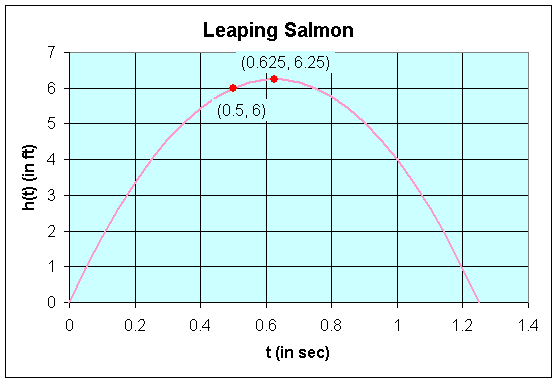
a. Sketch a graph of the height of the salmon (in feet), h(t), with time, showing clearly the maximum height and when the salmon can clear the wall.

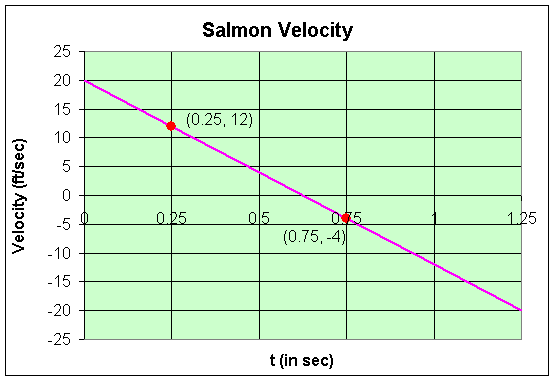
b. Find the average velocity of the salmon between t = 0 and t = 0.5 and associate this velocity with t = 0.25. Repeat this process for each half-second of the leaping salmon, then sketch a graph of the average velocity as a function of time, t.

c. Determine the minimum speed, v₀, that the salmon needs on exiting the water to climb the salmon ladder if the height is given by the formula

Solution: a. The function h(t) is a parabola, which can be written in the factored form of

It follows that the t-intercepts are t = 0 and t = 5/4 = 1.25. Thus, the vertex occurs at (0.625, 6.25). The graph of this parabola is seen below.

The salmon can clear the wall when h(t) = 6, so 20t - 16t² = 6 or 8t² - 10t + 3 = 0. This can be factored to give

It follows that either t = 1/2 or t = 3/4, so the salmon can clear the wall at any time 1/2 < t < 3/4 sec.

b. The average velocity of the salmon between t = 0 and t = 0.5 is given by

Similarly, the average velocity of the salmon between t = 0.5 and t = 1 is given by

The graph of the velocity curve is below

 

c. The minimum speed, v₀, that the salmon needs to climb the fish ladder is the one that produces a maximum height of 6 ft. This is equivalent to having the vertex of the height function occur with h = 6. Since h(t) = v₀t - 16t², the t-value of the vertex occurs at

(since this is halfway between the intercepts t = 0 and t = v₀ /16). Since we want the vertex to be 6 ft, we need to satisfy the equation

 

Thus,

Example 3 (Secant Lines): In this example, we examine a function, f(x), then form a sequence of secant lines by finding two points on the curve, then creating the line through those points. Consider the function

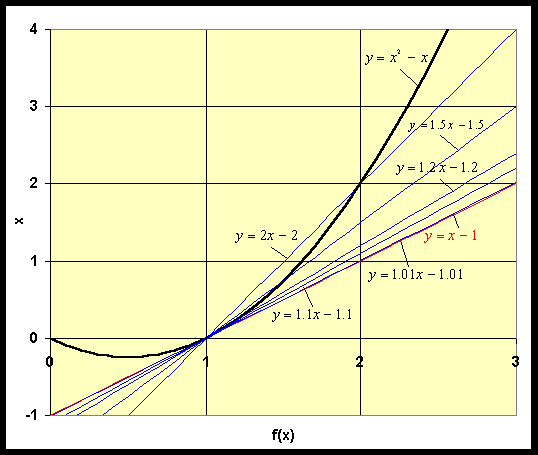
a. Let one point on all secant lines have x = 1. The other points in the sequence have x = 2, x = 1.5, x = 1.2, x = 1.1, and x = 1.01. Find the sequence of secant lines with these points on the line and on f(x).

b. The derivative of f(x) is the slope of the tangent line. As the values of x get closer together, the secant lines approach the tangent line. Use the results in Part a. to determine the equation of the tangent line through the point (1, 0), and from its slope find the derivative of f(x).

c. Graph f(x), the tangent line, and the secant lines.

Solution: a. The left point for all the secant lines is (1, 0). When x = 2, the other point is (2, 2). The equation of a line through (1, 0) and (2, 2) has a slope of 2 and y-intercept of -2, so its equation is given by

For x = 1.5, the points on the secant line (and f(x)) are (1, 0) and (1.5, 0.75). This secant line has a slope of m = (0.75 - 0)/(1.5 - 1) = 1.5. It follows that the equation for this secant line is

For x = 1.2, the points on the secant line (and f(x)) are (1, 0) and (1.2, 0.24). This secant line has a slope of m = (0.24 - 0)/(1.2 - 1) = 1.2, so the equation for this secant line is

For x = 1.1, the points on the secant line (and f(x)) are (1, 0) and (1.1, 0.11). This secant line has a slope of m = (0.11 - 0)/(1.1 - 1) = 1.1, so the equation for this secant line is

Finally, for x = 1.01, the points on the secant line (and f(x)) are (1, 0) and (1.01, 0.0101). This secant line has a slope of m = (0.01 - 0)/(1.01 - 1) = 1.01, and the equation for its secant line is

b. It is not hard to see that this sequence of secant lines is converging to the tangent line

The slope of this line is 1, so the derivative of f(x) = x² - x at x = 1 is also 1.

c. Below is a graph of the function, the tangent line, and our secant lines.

 

It becomes tedious calculating each of the elements of the sequence of secant lines as we saw in the previous example. The more general way to compute a secant line for a function f(x) at a point x is to find the equation of a line through the points (x, f(x)) and (x+ h, f(x+ h )), where h is some value different than zero.

Example 4(Secant line with h): Suppose we take the previous example and find the equation of the secant line through the points (2, f(2)) and (2+ h, f(2+ h)), where

Let h get small and determine the slope of the tangent line through (2, 2), which gives the value of the derivative of f(x) at x = 2.

Solution: The value of f(2+h) is given by

The slope of the secant line is given by

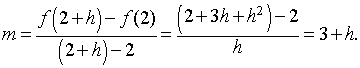
Using the point slope form of the line (with the point (2, 2) on the secant line), we find the equation of the secant line is given by

It is fairly easy to see that as h approaches zero, the secant line approaches the tangent line given by

This line has a slope of 3, so the derivative of f(x) at x = 2 must be 3.

Example 5 (Secant line for a Square Root): In this example, we consider a more complicated function. Suppose that

Find the slope of the secant line through the points (2, f(2)) and (2+ h, f(2+h)).

Let h get small and determine the slope of the tangent line through (2, 2), which gives the value of the derivative of f(x) at x = 2.

Solution: The slope of the secant line is given by

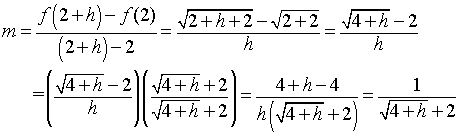
This formula is substantially more complex, requiring some techniques from algebra that you may have forgotten. This shows that finding the slope of the secant line can become quite tedious and difficult.

In the formula above, it is fairly easy to see that as h approaches zero, the slope of secant line, m, approaches

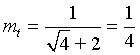
Since the derivative is related to the limiting case of the slope of the secant lines (the slope of the tangent line, m_t), we see that the derivative of f(x) at x = 2 must be 1/4.