Math 121 - Calculus for Biology I
Spring Semester, 2004
Chain Rule
San Diego State University -- This page last updated 19-Jan-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 19-Jan-04 |
|
In biology, there are often functional relationships where one measurable quantity depends on another, while the second quantity is a function of a third quantity. The first example below connects some of the ideas from previous sections on height and weight of girls, then creates a composite function to find the rate of change of weight with respect to age. This functional relationship uses composite functions. The differentiation of a composite function requires a special rule for differentiation, the chain rule.
Average Height and Weight of Girls
In the first section of the lecture notes, we
found that over a range of ages the rate of growth of girls in height remained
relatively constant. That is, the relationship between height and age was
approximated fairly well by a linear function. In the allometric section,
we saw that there is a power law relationship height and weight of animals,
so one would predict that a power law might work reasonably well for girls.
Below is a table of both heights and weights for average American girls between
the ages of 1 and 13.
|
age(years)
|
height(cm)
|
weight(kg)
|
|
1
|
75
|
9.5
|
|
2
|
87
|
11.8
|
|
3
|
94
|
15.0
|
|
4
|
102
|
15.9
|
|
5
|
108
|
18.2
|
|
6
|
114
|
20.0
|
|
7
|
121
|
21.8
|
|
8
|
126
|
25.0
|
|
9
|
132
|
29.1
|
|
10
|
138
|
32.7
|
|
11
|
144
|
37.3
|
|
12
|
151
|
41.4
|
|
13
|
156
|
46.8
|
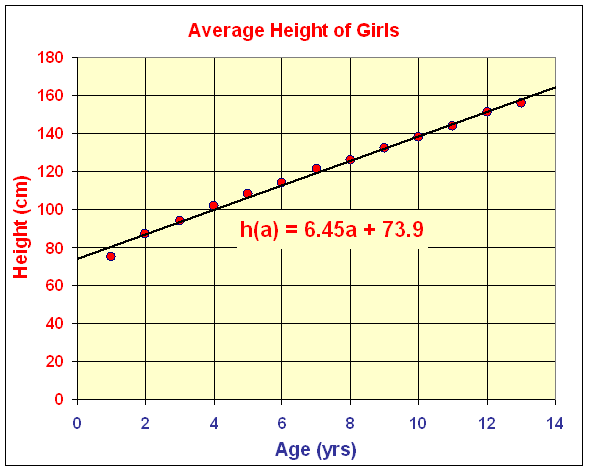
The height as a function of age is graphed below with the least squares best fit straight line for the data given by
h(a) = 6.45a + 73.9.
As noted in the linear modeling section, this equation shows that the average girl grows about 6.45 cm/yr.
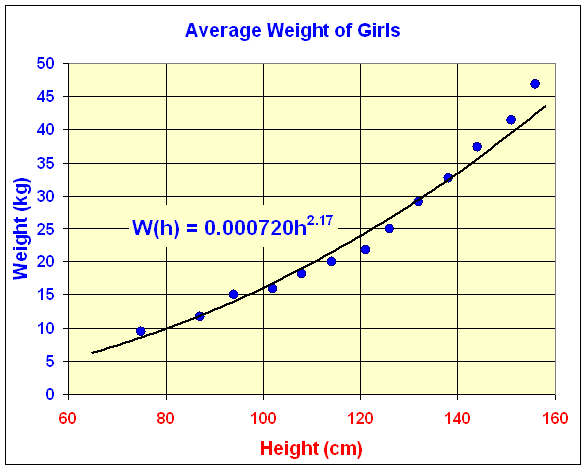
The relationship between the height and weight of a girl satisfies an allometric model. (This was demonstrated in the computer lab on the length and weight of dogs.) The average weight of a girl is plotted against her height below and fitted by the best allometric model through the data. The best equation is given by
W(h) = 0.000720h2.17.
With this information, we would like to connect these formulae and determine the rate of change in weight for a girl at any particular age (between 1 and 13). We will create a composite function to give the weight as a function of age, then use the chain rule to find the rate of change of weight with respect to age.
Consider the composite function f(g(x)). Suppose that both f(u) and u = g(x) are differentiable functions. The chain rule for differentiation of this composite function is given by
![]()
Another useful form of the chain rule is the differentiation formula given by
![]()
Example 1: Consider the function
h(x) = (x2 + 2x - 5)5.
Find h'(x).
Solution: This can be considered a composite of the function f(u) = u5 and the function g(x) = x2 + 2x - 5. It is easy to find the derivatives of both f and g. We have
f '(u) = 5u4 u' and g'(x) = 2x + 2.
From the formula above, we see that
Example 2: Consider the function
h(x) = exp(2-x2).
Find h'(x).
Solution: This can be considered a composite of the function f(u) = eu and the function g(x) = 2 - x2. The derivatives of f and g are
f '(u) = eu u' and g'(x) = -2x.
From the formula above, we see that
See the Worked Examples section for more examples.
From the data above, we found that the weight W as a function of height h is given by
W(h) = 0.000720h2.17.
while the height as a function of age is
h(a) = 6.45a + 73.9.
Because the height is a linear function the rate of change of height with respect to age is the constant 6.45 cm/yr. We will use the chain rule to find the rate of change of weight with respect to age, then graph both the weight as a function of age and the rate of change of weight as a function of age.
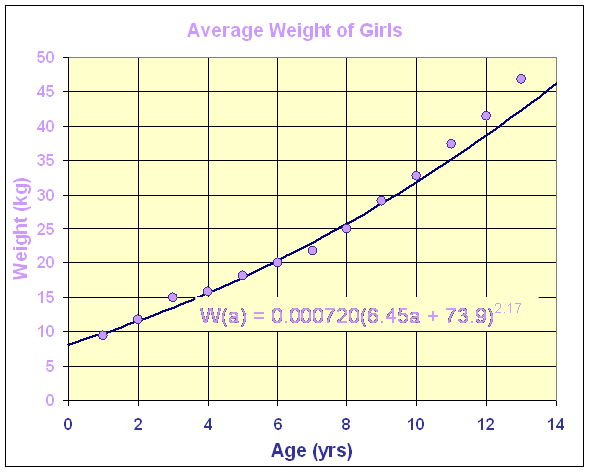
Writing weight as a composite function, we have
W(a) = 0.000720(6.45a + 73.9)2.17.
Below is a graph of this function with the data above.
By the chain rule, the derivative of the weight function is given by
![]()
with
![]()
Combining these and substituting the expression for h, we see that
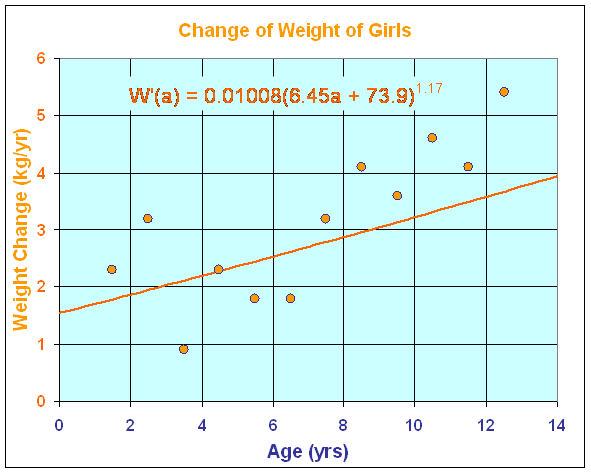
W '(a) = 0.01008(6.45a + 73.9)1.17.
Below is a graph of the derivative showing the rate of change in weight with respect to age. This graph is almost linear, since it is to the 1.17 power. The actual average weight changes are given for the data above. We see that the model underpredicts the weight gain for older girls.