Math 336 - Mathematical Modeling Spring Semester, 2000
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 14-Feb-00

1. Introduction
2. Malthusian Growth
3. Solution to the Malthusian Growth Model
4. Examples of Differential Equations
5. Classification of Type of Differential Equation
6. Problems

Introduction

Differential equations frequently arise in modeling situations.They can describe population growth, chemical reactions, heat exchange, motion, and many other applications. The previous sections have considered discrete dynamical systems, especially related to growth. Differential equations can be thought of as a continuous extension of the discrete dynamical systems.

A differential equation is any equation of some unknown function that involves some derivative of the unknown function. The classical example that first gave rise to differential Calculus is Newton's Law of motion. According to Newton's Law of motion, the mass of an object times its acceleration is equal to the sum of the forces acting on that object. However, acceleration is simply the first derivative of velocity or the second derivative of position. So Newton's Law of motion is an example of a differential equation. In biology, there are many applications of differential equations. Most frequently, a differential equation is describing either a growth rate or a reaction rate. In the upcoming sections, we will examine a collection of different applications.

Malthusian Growth

The first model we studied in discrete dynamical systems was the discrete Malthusian growth model. Recall that this model could be written

where P_n is the population at time n and r is the rate of growth. This equation can be rearranged to give

which says that the change in population between the (n + 1)^st time period and the n^th time period is proportional to the population at the n^th time period.

Now we want to write this model in terms of continuous time variables. Define P(t) to be the population at any time t. Assume that r is the rate of change of the population per unit time per animal in the population. If we let Dt be a small interval of time, then the change in population between t and t + Dt, satisfies the equation

Biologically, this equation says that the change (difference) in the population over a small period of time is found by taking the rate of growth times the population times the interval of time Dt. The equation above can be rearranged to give

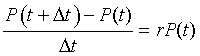
The right hand side of the equation readily transforms into a derivative as we take the limit of Dt tending toward zero. Thus, in the limit this model reduces to the differential equation

This is the continuous Malthusian growth model.

Solution to the Malthusian Growth Model

The differential equation describing the continuous Malthusian growth model says that the derivative of an unknown Population function P(t) is equal to a constant times the unknown Population function. (The rate of change of a population is proportional to the population.) The only function that we know that is a derivative of itself is the exponential function. We try a solution of the form

where c is an arbitrary constant. But P'(t) is cre^rt, which is rP(t), so satisfies the differential equation. If we add an initial condition P(0) = P₀, then the unique solution becomes

This is another reason why Malthusian growth is often called exponential growth.

Example 1: Consider the Malthusian growth model

Find the solution and determine how long it takes for this population to double.

Solution: From above we see that the solution is given by

This population doubles when 200 = 100e^0.02t . Thus, 0.02 t = ln(2) or t = 50 ln(2) = 34.66.

Examples of Differential Equations

 Examples:

 1. Radioactive Decay

Like the Malthusian growth model, this has an exponential solution, R(t) = R₀e^-kt.

2. Harmonic oscillator (often in spring mass problems, including vibrating cilia in ears)

Notice that the dependence of the dependent variable y is often suppressed in the statement of the differential equation. The general solution to this problem is y(t) = c₁cos(kt) + c₂ sin(kt), where c₁ and c₂ are arbitrary constants with y(t) being the position of the mass attached to a spring.

3. Swinging Pendulum

where y is the angle of the pendulum, m is the mass of the bob of the pendulum, and g is the gravitational constant.

4. Logistic Growth

where P is the population, r is the Malthusian rate of growth, and M is the carrying capacity of the population.

5. The van der Pol oscillator (often an approximation to nerve impulses)

where v is the voltage of the system and a and b are constants.

6. Lotka-Volterra - Predator and Prey model

where x is the prey species and y is the predator species with a, b, c, and d constants.

7. Forced Spring-Mass Problem with Damping

where y is the position of the mass, m is the mass of the object, c is the damping coefficient, k is the spring constant, and F(t) is an externally applied force.

Classification of Type of Differential Equation

The order of a differential equation is determined by the highest derivative in the differential equation. Thus, we see that in the examples above, Examples 2, 3, 5, and 7 are second order, while the others are first order. A differential equation is said to be linear if the unknown dependent variable and its derivatives only appear in a linear manner (i.e., they are to the first power). Examples 1, 2, and 7 are linear, while all the others are nonlinear. Good techniques exist to solve many linear differential equations, but few nonlinear problems have exact solutions. Example 6 is known as a system of first order differential equations. All of the examples except Example 7 do not have the dependent variable appearing in the differential equation, so these differential equations are said to be autonomous. Example 7 is a nonautonomous differential equation.

Problems:

 1. A population of bacteria begins with 1,000,000. The population is growing according to the Malthusian growth equation given by

where t is in minutes. Find how long it takes for this population to double. Find the population after one hour.

2. In the table below you are to find the solution of the differential equation in the left column from the list in the right column. Verify your choice. (The c is an arbitrary constant.)

y' = 1 - y	y(t) = c e2t
y' = -y	y(t) = c e-t + 1
y' = 1 - 2t	y(t) = c e-2t + t
y' = 2y	y(t) = c e-t
y' = 2ty	y(t) = 1 - c et
	y(t) = c exp(t2)
	y(t) = t - t2 + c

3. The table below has several second order differential equations in the left column. These have two independent solutions, which in the right column. Find the two solutions and verify your answers. (The c is an arbitrary constant.)

 

y'' + 4y = 0	y(t) = c e2t
y'' + 2y' + 2y = 0	y(t) = c cos(2t)
y'' - 4y = 0	y(t) = c e-t
y'' - y' + 2y = 0	y(t) = c e-t cos(t)
	y(t) = c e-2t
	y(t) = c sin(2t)
	y(t) = c et
	y(t) = c e-t sin(2t)