|
|
Math 122 Calculus for
Biology II |
16-Oct-12 |
|---|---|---|
|
|
|
|
|
|
Math 122 Calculus for
Biology II |
16-Oct-12 |
|---|---|---|
|
|
|
|
This page is designed to provide helpful information about the laboratory questions. This lab examines numerical techques for solving differential equations and reviews using Maple's dsolve. The first problem simply works with two diffferent differential equations to explore the numerical routines. The second problem explores drug responses in the body from two different ways of delivering teh drug. The last problem examines exposure to carbon monoxide using a mixing problem.
Problem 1: This problem is meant to give you practice with Euler's method and Improved Euler's method. The population model in the second part is a very common model, and it considers a time-varying growth rate, which is particularly important in modeling human populations or populations that experience human disturbances.
The numerical techniques given by Euler's Method and Improved Euler's Method are used to approximate solutions to differential equations using a simple discrete algorithm. For each method you will be given a differential equation of the form:
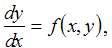
a step size given by h and an initial condition y(0) = y0. Given the fact that both numerical methods are discrete formula much like the discrete dynamical models from earlier this semester, it is easy to work with Euler's and Improved Euler's method in Excel.
We will begin by constructing a
column for xn,
a column for yn
and then finally a column for f(xn,yn).
In the first row
of our Excel sheet we want to input the initial x = x0
and y = y0
values. In the f(xn,yn)
column we want to calculate the
value of the differential equation at x0
and y0.
Example:
If we had the
problem:
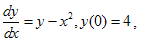
then we would fill in the first row of our Excel sheet as follows:
| x(n) | y(n) | f(x(n), y(n)) |
| 0 | 4 | = B2 - A2^2 |
Euler's Method
We are now ready to set up the rest of the discrete model for Euler's Method. Geometrically, Euler's method starts at the initial point , y0, then it uses the direction of the derivative to step a distance, h, and project the next guess at where the solution should be. It proceeds in a similar manner at each step moving a distance forward h in the x direction and using the derivative at the new position to move in a straight line direction to the next y value. Thus, in the xn column we want to produce x values the go up by our given step size h. (In the following, you can either create a named variable h, or insert your value of h. The former gives you a more general Euler's method to continue for varying the stepsize.) So in the cell below the initial x value we type in the formula '=A2+h'. We have now created the x1 term. Euler's Method is given by the equation
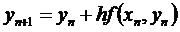
So in the cell below the
initial y
values
we type in the formula: '=B2+h*C2'.
Remember that the B column in this example represents our y
values
and the C column represents the value of our differential
equation. In the final column for f(xn,yn)
(the derivative or direction of the solution at (xn,yn)),
we want to
once again calculate the value of the differential equation
for xn
and yn
so we use the same formula
we used in cell C2. We
are now ready to simulate Euler's Formula for as many steps as we would
like. We simply highlight all three cells (A2, B2, and C2 in
our example) and click and drag down until we've reached the
final xn
value.
| A | B | C | |
| 1 | x(n) | y(n) | f(x(n), y(n)) |
| 2 | 0 | 4 | = B2 - A2^2 |
| 3 | =A2 + h | =B2 + h*C2 | = B3 - A3^2 |
| : | : | : | : |
Improved Euler's Method
The Improved Euler's Method uses an intermediate step to improve the accuracy of the approximation (significantly). In this case, instead of fitting a straight line in the direction of the solution, it uses a mathematical trick to fit the best quadratic in the direction of the solution. Computationally, this means that we need to do one more function evaluation to get a much better numerical solution. This is accomplished in Excel by adding two more columns: one that has the Euler solution ye and another column that gives the improved update to the derivative using the updated time and Euler's solution. The first three columns of this method are constructed in a similar way as the normal Euler's formula. In the fourth column we input the normal Euler's model, i.e., '=B2+h*C2'. Notice that instead of putting this formula in the cell just below the last yn value we are now putting it in its own column. In the fifth column we insert the improved calculation for the derivative given by f(xn+h, ye). The new value for y in the second column below this row uses an average of the Euler approximation of the derivative and the updated Improved Euler approximation of the derivative. The new updating function to approximate the solution of the differential equation using the Improved Euler's Method in the cell below the yn term is given by the formula:
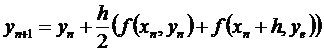
This formula uses the same idea as Euler's Formula, except instead of simply moving a step in the direction of the derivative, a correction is made while moving that step to account for nonlinear changes in the function f. In Excel the code in the cell B3 (just below the initial y value) would be '=B2+(h/2)*(C2+(D2-(A2+h)^2)). Notice that the last piece of the formula (D2-(A2+h)^2) is simply f(xn+h, ye). The rest of the code is the same and we can then click and drag the row to produce results to any xn we would like:
| A | B | C | D | E | |
| 1 | x(n) | y(n) | f(x(n), y(n)) | ye | f(x(n)+h, ye) |
| 2 | 0 | 4 | = B2 - A2^2 | = B2 + h C2 | = D2 - (A2+h)^2 |
| 3 | =A2 + h | =B2 + (h/2)*(C2 + E2) | = B3 - A3^2 | = B3 + h C3 | = D3 - (A3+h)^2 |
| : | : | : | : | : | : |
In the lab you will compare your numerical solution to the actual solution, which in both cases is a separable differential equation. At the time of writing this lab, we have not solved these in class, but will be doing so very shortly. For this lab, you should let Maple solve the differential equation, using Maple's dsolve routine.
To solve the differential equations using Maple, you can apply Maple's dsolve routine. The Malthusian growth model is used as an example below. The commands to solve this differential equation are simply:
>
de :=
diff(P(t),t)= r*P(t);
# This
allows you to view the
differential equation.
>
dsolve({de, P(0) =
P0}, P(t));
# This solves the
differential equation with an
initial condition.
>
simplify(%);
# This puts the solution in a simpler form.
>
p :=
unapply(rhs(%),t);
# This
stores the solution as the function p(t).
Problem 2 : This question examines how drugs can be absorbed into the body through different delivery systems. The advent of polymers that dissolve safely in the body allows the administration of drugs, such as Norplant for extended birth control. Getting the appropriate doses with this new technology requires some careful analysis of both theoretical models and experimental tests. This problem examines some of the simplest theoretical models.
Part a should be very easy as it is like the radioactive decay problems. Part b has a differential equation that we will not be solving in class. This will once again require that you use Maple's dsolve command to solve this differential equation. Once you have the solution to this differential equation, the problem should be quite easy. You can find the maximum either by techniques learned in class or by lab techniques with Maple.
The last part of this problem continues the numerical techniques for differential equations. Once again you will be solving the differential equation using Excel, and the improved Euler's method routines that you explored in the first problem can be readily used for this problem. (The actual solution was found in Part b.) You will compare your numerical solution to the actual solution to determine how well numerical solutions can suffice for many practical examples.
Problem 3 : This problem is very much like the lake pollution problems that you have studied in class. For example, you may want to consult the discussion of the lake pollution problem at the beginning of the numerical section for differential equations. The techniques for numerically solving this problem are very similar to the techniques used in the previous problems.