|
|
Math 241 - Maple Workshop |
|
|---|---|---|
|
San Diego State University -- This page last updated 13-Oct-03 |
This session will examine several graphics routines with vector Calculus, then show how Maple can be applied to differential equations. Data is fit to a cubic polynomial, then graphed. 3-D surfaces are plotted, then the volume and surface integrals are analyzed. The Divergence and Stokes' Theorems are visualized, then special functions, including gradient and curl are applied. We include the LaTeX command to show how to generate latex code for good document presentation. The graphics ends with animations of Fourier series and a parametrized 3-D surface. As usual, there is a hyperlink to the Maple Worksheet for this lecture.
Vectors
We begin with some basic vector operations.
> a := [2, -1, 5]; b := [1, 3, -4]; c := Vector[row](3,-2);
![]()
![]()
![]()
Adding vectors is easy, but different forms may require the evalm (matrix evaluation) command.
> a+b;evalm(a+b-c);
![]()
![]()
Many of the operations with vectors require one of the Maple special packages, linalg or LinearAlgebra.
> with(linalg):
Below we show the dot or inner product and the cross product.
> dotprod(a,b); innerprod(a,c);
![]()
> crossprod(a,b);
![]()
Next we enter a vector function, then take the divergence and curl of this function.
> F := (x,y,z) -> [x^2*cos(y*z),-x^2*z*exp(y^2),ln(x)/(z*y)];
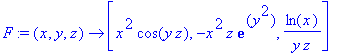
> diverge(F(x,y,z),[x,y,z]);
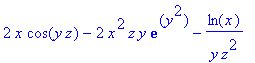
> curl(F(x,y,z),[x,y,z]);
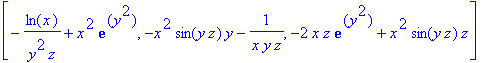
Graphics
Maple's graphics capabilities cover a variety areas using several special packages. These require special tools and some are shown below.
Fitting Data
Suppose we want to fit data to a cubic model and visualize both the data and the model. Our example comes from the oxygen consumption of the "kissing bug," Triatoma phyllosoma , during the fourth instar stage (Data from Boyd Collier). This bug carries chagas disease. The time data (in hours) is stored as td, while the oxygen consumption is stored as yd.
> td := [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]: yd := [116.6, 120.1, 114.9, 129.9, 116.5, 107.7, 99.0, 104.0, 100.7, 87.5, 82.7, 53.8, 54.0, 72.4, 81.1]:
We will use the statistics package (for least squares), the statistics plotting package (for scatterplot), and the plotting package (for displaying two types of graphs).
> with(stats): with(stats[statplots]): with(plots):
Graph the data with circles for points, then store this graph for later. First view the graph, then store the picture.
> plots[display](scatterplot(td,yd),symbol=circle);
![[Maple Plot]](images/session31.gif)
> Data := plots[display](scatterplot(td,yd),symbol=circle):
> model := a*t^3 + b*t^2 + c*t + d;
Find the least squares best fit of the cubic model to the data.
> eqn := fit[leastsquare[[t,y], y=model, {a,b,c,d}]]([td, yd]);
Make y into a function depending on t .
> y := unapply(rhs(eqn),t);
Store the graph of the model, then display it with the graph of the data.
> Y := plot(y(t),t=0..15):
> display({Data,Y});
![[Maple Plot]](images/session35.gif)
Select individual coefficients from the model.
> b := coeff(y(t),t,2);
Volume and Surface Area
Maple provides a good tool for visualizing the 3-D surfaces from vector Calculus. It can be readily used to find the surface area and volume of these 3-D objects. Consider the following paraboloid.
To visualize this surface in Maple, we need to parameterize the x , y , and z components into 2 parameters. I want the graph centered on the origin (axes = NORMAL) and the picture unscaled (scaling = CONSTRAINED).
> r := [u*cos(v)/2,u*sin(v),4-u^2];
> plot3d([r[1],r[2],r[3]],u=0..2,v=0..2*Pi,axes = NORMAL, labels = [x,y,z], scaling = CONSTRAINED, orientation = [40,70]);
![[Maple Plot]](images/session38.gif)
We find the volume under this surface (using symmetry).
> 4*Int(Int(4-4*x^2-y^2,y=0..sqrt(4-4*x^2)),x=0..1);
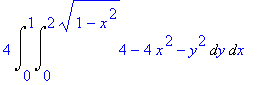
The formula can be inserted into a LaTeX document by letting Maple generate the code.
> latex(%);
4\,\int _{0}^{1}\!\int _{0}^{2\,\sqrt {1-{x}^{2}}}\!4-4\,{x}^{2}-{y}^{
2}{dy}\,{dx}
Below we compute the double integral.
> 4*int(int(4-4*x^2-y^2,y=0..sqrt(4-4*x^2)),x=0..1);
We find the surface area of this surface (again using symmetry). A reminder that if z = f ( x , y ), then the formula for computing the area of the surface is
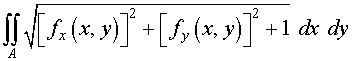
> f := (x,y) -> 4 - 4*x^2 - y^2;
> 4*Int(Int(sqrt((diff(f(x,y),x))^2+(diff(f(x,y),y))^2+1),y=0..sqrt(4-4*x^2)),x=0..1);
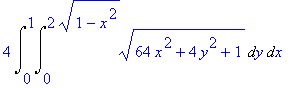
> 4*int(int(sqrt((diff(f(x,y),x))^2+(diff(f(x,y),y))^2+1),y=0..sqrt(4-4*x^2)),x=0..1);
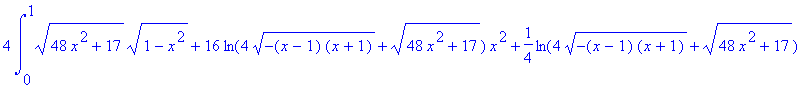
![]()
> evalf(%);
An alternate method for computing surface integrals uses the following formula
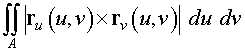
> with(linalg):
We created the parametrized surface by the function r ( u , v ) given above. By taking the crossproduct of the partial derivatives of the parametrized surface function, we obtain the outward normal to the surface.
> ruxrv := crossprod(diff(r,u),diff(r,v));
> absruxrv := sqrt(ruxrv[1]^2 + ruxrv[2]^2 + ruxrv[3]^2);
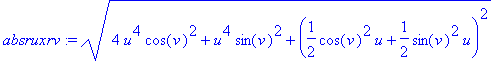
The area of the surface is the integral over the range of the parameters of the magnitude of the outward normal. One could use the norm function, but Maple has difficulty integrating quantities with absolute values.
> int(int(absruxrv, u = 0..2),v = 0..2*Pi);
![]()
![]()
Often when the integral cannot be evaluated exactly, the evalf function allows numerical solution of the integral.
> evalf(%);
Gauss' and Stokes' Theorems
Two of the major theorems used for fluid flow are the Divergence or Gauss' Theorem and Stokes' Theorem. The Divergence Theorem provides an means of determining the flow through a bounded region in 3-space. Stokes' Theorem gives information on the rotation of a fluid.
Let us consider these theorems for a fluid flowing through a hemisphere. We begin by visualizing the fluid flow and the hemisphere.
> with(plots):
View the fluid flow, using Maple's fieldplot.
> F := [x^2*y, y*z, 2*z-1];
>
fieldplot3d(F,x=-4..4,y=-4..4,z=-1..4,grid=[8,8,5],axes
= NORMAL, thickness = 2);
Flow :=
fieldplot3d(F,x=-4..4,y=-4..4,z=-1..4,grid=[8,8,5],axes =
NORMAL, thickness = 2):
![[Maple Plot]](images/session322.gif)
Graph the hemisphere, which is the surface bounding the region for applying the Divergence and Stokes' Theorem.
> r := [3*cos(u)*cos(v),3*sin(u)*cos(v),3*sin(v)];
>
plot3d([r[1],r[2],r[3]],u=0..2*Pi,v=0..Pi/2,axes
= NORMAL, labels = [x,y,z], orientation = [40,70],
style = WIREFRAME, color = BLACK);
Hemi :=
plot3d([r[1],r[2],r[3]],u=0..2*Pi,v=0..Pi/2,axes
= NORMAL, labels = [x,y,z], scaling = CONSTRAINED,
orientation = [40,70], style = WIREFRAME, color =
BLACK):
![[Maple Plot]](images/session324.gif)
> display3d({Flow,Hemi});
![[Maple Plot]](images/session325.gif)
The Divergence Theorem is given by
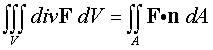
The easiest way to solve the second integral is to parametrize the surface A, as A = r(u,v), then use this parameterization to find the normal to the surface,
![]()
The integral becomes
![]()
> with(linalg):
Here we compute the divergence of the vector flow field, then integrate this quantity over the volume.
> divF := diverge(F,[x,y,z]);
> Int(Int(Int(divF,z = 0..sqrt(9-x^2-y^2)),y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);
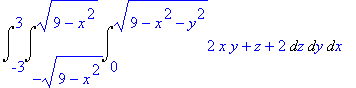
> int(int(int(divF,z = 0..sqrt(9-x^2-y^2)),y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);
> evalf(%);
The above integral is more easily written in spherical coordinates and given by
> Int(Int(Int((2*rho^2*cos(theta)*sin(theta)*sin(phi)^2 + rho*cos(phi) + 2)*rho^2*sin(phi),rho = 0..3),theta = 0..2*Pi),phi = 0..Pi/2);
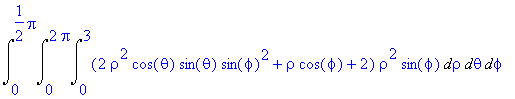
> int(int(int((2*rho^2*cos(theta)*sin(theta)*sin(phi)^2 + rho*cos(phi) + 2)*rho^2*sin(phi),rho = 0..3),theta = 0..2*Pi),phi = 0..Pi/2);
> evalf(%);
Stokes' Theorem measures the circulation around any curve C . If we consider the curve where the hemisphere intersects the xy -plane with the flow F given above, then Stokes' Theorem states that
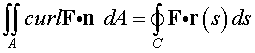
The integral on the right is most easily solved using the technique above for the Divergence Theorem. Parametrize the surface A = r(u,v), then use this parameterization to find the normal to the surface,
![]()
The double integral becomes the same as above with curl F replacing F.
Here we compute the curl of the vector field, then evaluate the double integral over the circle in the xy -plane beneath the hemisphere.
> curlF := curl(F,[x,y,z]);
> curlFn := dotprod(curlF,[0,0,1]);
> Int(Int(curlFn,y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);
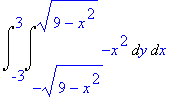
> int(int(curlFn,y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);
In polar coordinates...
> int(int(-R^3*cos(theta)^2,R = 0..3),theta = 0..2*Pi);
Animations
Maple has programs that allow visualization of 2 and 3-D graphics through animations.
We begin with a repeat of our Fourier series expansion from the previous session. However, this time, the evolution of the partial sums of the Fourier series is viewed through animation, which allows one to easily see how the Fourier series is converging. The animation program requires the plots package.
> with(plots):
> bi := int(x*sin(i*Pi*x),x=-1..1);
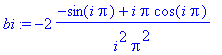
> S := n -> sum(bi*sin(i*Pi*x), i = 1..n);
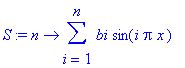
> animate(S(n), x=-3..3,n=1..20,frames=20,numpoints=500, color = blue);
![[Maple Plot]](images/session340.gif)
After invoking the animation, a series of buttons appears on the menu bar. These allow the user to view the movie of the graph evolving either forward or backward, cycle through, or go frame by frame.
Below we simply took one of the 3-D examples from Maple's Help. In the 3-D case, the default uses just 8 frames.
> animate3d(cos(t*x)*sin(t*y),x=-Pi..Pi, y=-Pi..Pi,t=1..2,color=cos(x*y));
![[Maple Plot]](images/session341.gif)