Solution by Separation of Variables

The classical method of solution for such BVPs is the method of separation of variables . Assume a solution of the separated form

a product of one function just containing x and one function just containing t . Recall the initial example

from above.

Now, generalize this to the product , that is, to

> U := X(x)*T(t);

>

to which we next apply the fixed endpoint conditions, obtaining

and

that is,

> subs(x=0,U) = 0;
subs(x=L,U) = 0;

>

Ruling out the choice because that implies = 0 (identically), we conclude = 0.

Under the assumption of a separated solution, the initial conditions become

=

ans

T'(0) =

Unless either or is zero, no conclusion can be drawn from these two equations. Assuming for simplicity that the initial velocity is zero, so that , we conclude

= X(x) T'(0) = 0 => T'(0) = 0

The initial condition can be satisfied with the aid of a Fourier series. Before we can see that, we must apply the separation assumption to the PDE itself, namely

> q := diff(u(x,t),t,t) = c^2*diff(u(x,t),x,x);

>

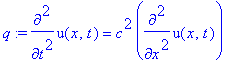
giving

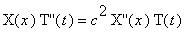
that is,

> q1 := eval(subs(u(x,t)=U,q));

>

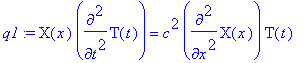
We have just deliberately committed a notational no-no. The derivatives on the left are with respect to , while the derivatives on the right are with respect to . Yet, we have used the same symbol for each differentiation, a mathematical imprecision and ambiguity that is too convenient to avoid.

Next, divide by 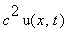, with in the form

This general strategy, which seems to work with linear second-order PDEs, gives

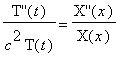
that is,

> q2 := q1/(c^2*U);

>

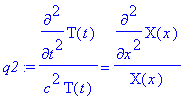
the separated form of the PDE wherein each side of the equation is a function of only one of the variables. Since on the left there is a function purely of t , and on the right, a function purely of x , and these two functions must be equal for all values of x and t , each must be equal to the same constant.

This argument is generally not transparent to the novice. Consider the following. Student A is asked to state a "favorite function of ." Student B is asked to state a "favorite function of ." Typically, the functions now written on the board are something like and . Student C is asked to select a "favorite value of ," and student D is asked for a "favorite value of ." The functions and are now computed at values such as and . The students then realize that because 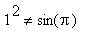= 0, the only way for a function of to equal, consistently, a function of is for the two functions to be the same constant function.

This constant is typically taken as and is called the Bernoulli separation constant . Hence, we have the two ordinary differential equations

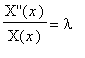
and

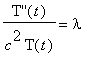
which, together with the relevant data, form the two problems

= 0

and

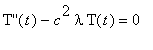
The first problem is a Sturm-Liouville eigenvalue problem, while the second is a modified initial value problem.

Obtaining the two separated ordinary differential equations in Maple is not a simple task. For example, we begin with

> q3 := rhs(q2) = lambda;
q4 := lhs(q2) = lambda;

>

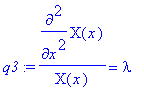
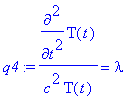
Then, re-arranging, we get

> q5 := lhs(X(x)*q3) - rhs(X(x)*q3) = 0;
q6 := lhs(c^2*T(t)*q4) - rhs(c^2*T(t)*q4) = 0;

>

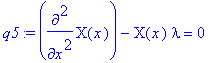
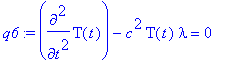
In effect, we did all the work. Maple really only played the role of bookkeeper, because it does not have any built-in code for performing manipulations of this type.

The solution of this Sturm-Liouville eigenvalue problem, obtained in Section 16.1, is

with eigenvalues

Again, Maple presently does not have the tools with which to construct these solutions, so we enter them as

> Xn := B[n]*sin(n*Pi*x/L);

>

with eigenvalues given by

> lambda[n] := -(n*Pi/L)^2;

>

for , ....

For each value of , the function T( ) is the solution of

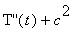
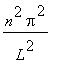
so we write

a solution we obtain in Maple by writing the differential equation as

> q7 := subs(lambda=lambda[n],q6);

>

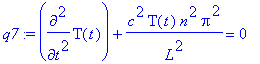
then solving with

> q8 := dsolve({q7,D(T)(0)=0},T(t));

>

Emphasizing the dependence on , we write

> Tn := subs(_C2=C[n],rhs(q8));

>

( Caution : If Maple uses _C1 instead of _C2 for the constant of integration, please adjust the worksheet accordingly.)

A single eigenfunction, is therefore the product

that is,

> Un := Xn*Tn;

>

which contains two constants where only one is needed. Hence, replace the product with the single constant via

> un := algsubs(B[n]*C[n]=b[n],Un);

>

The set of eigensolutions can be thought of as the analog of a fundamental set for a linear ODE. The general solution of a linear ODE is a linear combination of all the members of the fundamental set. Similarly, the most general solution of the linear PDE is a linear combination of all the members of its "fundamental set," namely, the set of eigensolutions .

Since there are an infinite number of eigensolutions, our general solution is the infinite sum

=

that is,

> U := Sum(un,n=1..infinity);

>

The final condition to be applied in this BVP is the initial shape requirement,

=

that is,

> simplify(subs(t=0,U)) = f(x);

>

The coefficients must therefore be the Fourier sine series coefficients for the function . There is no other choice for these constants if this final condition is to be satisfied. If is to be equal to a sum of sine terms, then the coefficients in that sum must be the Fourier sine series coefficients. Therefore, the 's are determined by the Fourier sine series formulas

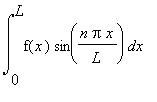
and the solution is given by the infinite series

This infinite sum, along with the defining integrals for the , constitutes the formal solution to the given BVP for the finite plucked string.

>