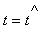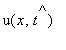Wave Equation on the Finite String

An idealized string, uniform and without internal friction, is stretched along an -axis from to . The ends are fixed, the string is taut, and it is constrained to move in a vertical plane. The equilibrium position for the string coincides with the interval on the -axis, and displacements in the string are measured vertically by . At time , and at location in , the displacement of the string from equilibrium is . For fixed 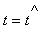, the shape of the string is given by .

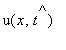Figure 24.1, below, shows the shape of the string at a particular instant .

> p1 := plot(x*(1-x),x=0..1,color=black):
p2 := textplot([1,-.05,`L`], font=[TIMES,ITALIC,12]):
p3 := arrow([.5,.09],[.5,0],.01,.03,.2,color=black):
p4 := arrow([.5,.16],[.5,.25],.01,.03,.2,color=black):
p5 := textplot([.5,.125,`u(x,t)`]):
### WARNING: note that `I` is no longer of type `^`
p6 := textplot([.525,.136,`^`]):
display([p||(1..6)],scaling=constrained, labels=[x,u], xtickmarks=[-1,2], ytickmarks=[-1,1], labelfont=[TIMES,ITALIC,12]);

>

Wave Equation (1) for

fixed left end (2)

fixed right end (3)

initial shape (4)

initial velocity (5)

__________________________________________________

Table 24.1

As we will derive in Section 24.4, displacements in the string are governed by , the wave equation (1) in Table 24.1. This is a partial differential equation (PDE) in the two independent variables and . The parameter will turn out to be the wave speed , the speed at which a disturbance can propagate horizontally along the string. The boundary conditions (2) and (3) in Table 24.1 assure that the endpoints of the string remain fized. Because they proscribe values of at the endpoints, they are called Dirichlet conditions. Since the prescribed values are zero, these conditions are homogeneous Dirichlet conditions. The initial conditions (4) and (5) in Table 24.1 give the initial shape and velocity of the string. At first, we will take , so that the string is given a (small) initial displacement , and released. This corresponds to a gentle plucking of the string, much like the action in a harpsichord.

Together, the five equations in Table 24.1 constitute an initial-boundary value problem (or BVP) for the finite string. Our goal is to obtain a solution to this BVP, and to understand how the function so determined describes the physical motion of the string.

>