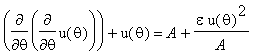
What happens when we consider the effects of General Relativity?

Starting from the Schwarzchild metric one can show that our equation of motion is modified to:

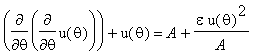
Here epsilon (a small amount) is given in terms of G , M , and c as defined above.

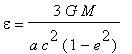
Our equation has an additional inhomogeneous term which is proportional to u^2 and consequently the DE is non linear. In the rest of this Maple session we will use a method of Kryloff and Bogoliuboff to find a series solution and thus calculate the precession rate of Mercury as predicted by General Relativity.

First we use the alias command to ensure the output is printed correctly.

> alias(w[0]=w0, w[1]=w1,u[0]=u0,u[1]=u1);

First we set up the basic differential equation governing the planetary orbits in General Relativity

> eq:= diff(u(theta),theta$2) + (w[0]^2)*u(theta) = A + epsilon*u(theta)^2/A;

Here u = 1/r where r is the distance from the planet to the Sun, epsilon is defined as above, and A is a non-relativistic inhomogeneous term (i.e. constant).

Let's solve for w[0]=1 and epsilon=0 (a non-relativistic limit).

> dsolve(subs(epsilon=0,w[0]=1,%), u(theta));

So the zero-order solution is that of a simple harmonic oscillator with a natural angular frequency w[0]=1 plus a constant. The MAPLE constants _C1 and _C2 are arbitrary.

Thus for non-relativistic Keplerian motion, r(theta) returns exactly to it's original position every 2 Pi radians. However the non-linear term will cause a frequency shift from w[0]=1 and consequently cause a precession.

We now get a series solution in powers of "epsilon" using the method of Kryloff and Bogoliuboff:

Expand u(theta) and frequency w[0] :

+ ...

+ ...

We achieve this as follows:

> eval( subs( u(theta)=u[0](theta)+epsilon*u[1](theta), eq ) );

> subs(w[0]^2=w^2+epsilon*w[1]+epsilon^2*w[2],%):

We obtain a series expansion in epsilon on both sides

> eqs:=map(series,%,epsilon, 2);

Collect the zero-order equation in eq[0],

> eq[0]:=coeff(lhs(eqs),epsilon,0)= coeff(rhs(eqs),epsilon,0);

and the first order equation in eq[1].

> eq[1]:=coeff(lhs(eqs),epsilon,1)= coeff(rhs(eqs),epsilon,1);

Now solve the zero-order equation.

> dsolve(eq[0],u[0](theta));

We obtain essentially the same solution as before. We will assign this solution to u[0] and simplify it by insisting that the angle theta be measured from the position of the perihelion (i.e. u[0] is a maximum at theta=0).

> assign(%);

We find the derivative w.r.t. theta of u[0](theta) at theta =0.

> eval(subs(theta=0,diff(u[0](theta),theta)));

Thus to insure u[0](theta) is a maximum at theta=0 we set the constant _C2 to zero.

> _C2:=0:

Next we solve the first-order equation after simplifying the inhomogeneous term. We use combine with it's trigonometry option to do so.

> eq[1]:=combine( eval(eq[1]) , trig );

> dsolve( eq[1], u[1](theta) );

Maple has given us a particular solution plus a complementary solution with arbitrary constants _C3 and _C4, which we don't need, and thus throw away:

> subs (_C3=0, _C4=0, %):

Now we collect in theta.

> collect( combine( % , trig) , theta );

We note that Maple has not made the simplification

This is of course correct, since arctan(tan(x))=x is not true in general. In this case it is OK to make the simplification, so we do.

> arctan(sin(w*theta/2)/cos(w*theta/2)):=w*theta/2;

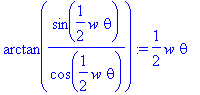
> collect(%%,theta);

Now we notice terms like cos(theta) and cos(2*theta) and these represent a small periodic disturbance of the normal Keplerian motion. They will not contribute on average. However, the term proportional to "theta" is secular and therefore observable effects arise on an sufficiently long period of time. So we grab this term.

> op(1,rhs(%));

We solve for w[1] such that this term is zero.

> w[1] := solve( % , w[1] );

To first-order in epsilon, we can isolate a value for w.

> ### WARNING: persistent store makes one-argument readlib obsolete
readlib(isolate):

> isolate( w[0]^2 = w^2 + w[1]*epsilon , w );

And w[0]=1 and to first-order in epsilon the effective frequency w is

> simplify( subs( w[0]=1 , w = series(rhs(%),epsilon,2) ) );

> assign(%);

Thus cos(w theta) has a maximum when

> w*theta = 2*Pi*n;

Where n is a non-negative integer. Let's isolate theta.

> isolate(%,theta);

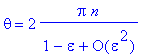
To first order in "epsilon", this is just

> lhs(%) = series(rhs(%),epsilon,2);

Thus the successive perihelia do not appear at intervals of 2 Pi but, rather of 2 Pi + delta which is given by the second term on the right.

> delta:=subs(n=1,coeff(rhs(%),epsilon,1))*epsilon;

Substituting the value of epsilon in the above

> delta:=subs(epsilon = 3*G*M/(a*c^2*(1-e^2)),%);

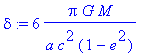
Finally, we get the well-known formula for the perihelion precession rate.

We see therefore that the effect is enhanced if the semimajor axis a is small and the eccentricity "e" is large. Mercury, which is the planet nearest the Sun and which has the most eccentric orbit of any planet (after Pluto), provides the most sensitive test of the theory.

Next we plug in values for the gravitational constant G and the sun's mass M.

> subs(G=6.672*(10^(-11)),M=1.99*(10^(30)),%):

Then, plug in quantities for the orbit parameters of Mercury

> delta[Mercury]:=subs(e=.2056, a=.3871*1.495*(10^11),c=2.997925*(10^8),%);

Now this is a very small arc, so we consider the change of arc over a century. In this case, Mercury will have made (100/T) revolutions and the result in radians has to be converted into seconds of arc. T is the period of orbit.

> T:=0.2408:

> evalf(3600*(360/(2*Pi))*(100/T)*delta[Mercury],4);

>