Optimization

1. Crow Predation on Whelks
2. Mathematical Model for Energy
3. Optimal Solution
4. Optimal Study Area
5. Worked Examples
6. Chemical Reaction
7. References

In biology, animals are frequently devising optimal strategies to gain advantage. These might result in reproducing more rapidly, or better protection from predation. It has been argued that primitive animals long ago split into the prokaryotes (bacterial cells) and eukaryotes (cells in higher organisms like yeast or humans) from a common ancestor, which had elements of both. One argument contends that eukaryotic cells added complexity, size, and organization for advantage in competition, while the prokaryotes stripped down their genome (eliminated "junk" DNA) to the minimum required for survival, to maximize reproduction. These arguments suggest that organisms try to optimize their situation to gain an advantage.

The derivative was a valuable tool in finding critical points on graphs. These critical points were local minima or maxima for the function. This is one of the valuable applications of Calculus, where an optimal solution is found for some problem.

Crow Predation on Whelks

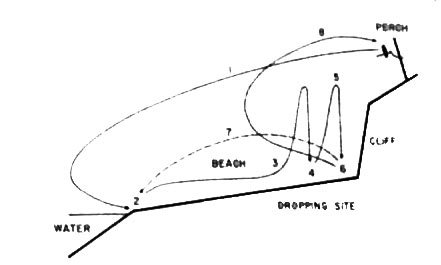
Sea gulls and crows have learned to feed on various mollusks by dropping their prey on rocks to break the protective shells. Reto Zach performed a detailed study of Northwestern crows (Corvus caurinus) on Mandarte Island, British Columbia to learn more about their habit of selecting and consuming whelks (Thais lamellosa). Some ecologists argue that studies on the behavior of such interactions gives insight into the decision making of optimal foraging.

Zach observed that Northwestern crows, perched above the beaches, flew to the intertidal zone and searched carefully for the largest whelks they could find. After selecting a whelk (occasionally more than one), the crows flew to a favorite rocky area, where they flew vertically upwards and released the whelk. The whelk would hit the rocks. If the whelk split open, the crow would remove the edible parts. However, if it failed to break, the crow would seize the whelk again, fly vertically, and drop the whelk again, repeating this process until the whelk broke open and could be consumed. (One crow took 20 drops to open one whelk.) Zach observed that the crows usually flew to height of 5 meters with little variation. He also noted that it took a little over 4 drops on average for the whelks to break open. Can this behavior be explained by an optimal foraging decision process? Is the crow exhibiting a behavior that minimizes its expenditure of energy to feed on whelks?

In Zach's first experiment, he selected a collection of whelks and sorted them according to size (small, medium, and large). He then dropped these whelks from various heights until they broke, and recorded how many drops at each height were required to break each whelk. A graph of his results is shown below.

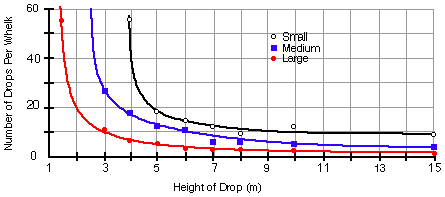
Notice that it is clearly easier to break open larger whelks, and another experiment confirmed that crows selectively chose the largest available whelks. It was noted that there was a gradient of whelk size on the beach, suggesting that the crows' foraging behavior was affecting the distribution of whelks in the intertidal zone, with larger whelks further out. If the larger whelks are easier to break open, then clearly the crows benefit by selecting the larger ones because they don't need as many drops per whelk, and they gain more energy from consuming a larger one. The study showed that the whelks broken on the rocks were remarkably similar in size, with the average whelk weighing about 9 grams.

Next, Zach observed the height of the drops and number of drops required for many crows eating whelks, using a marked pole on the beach near a favorite dropping location. Below are histograms of his observations.
 
 

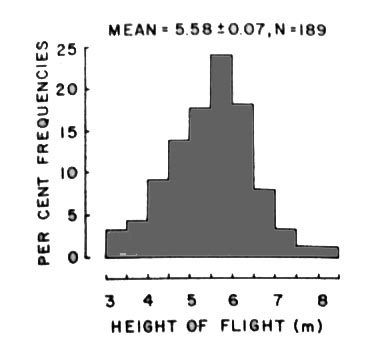
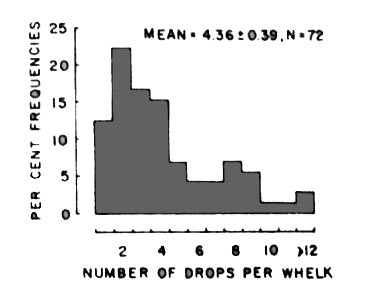
So why do the crows consistently fly to about 5.25 m and use about 4.4 drops to split open a whelk? Can this be explained by a mathematical model for minimizing the energy spent, thus supporting an optimal foraging strategy?

Mathematical Model for Energy

From Physics, we know that the energy is directly proportional to the vertical height that an object is lifted. (This is commonly called the work put into a system.) Thus, the energy that a crow expends breaking open a whelk depends on the amount of time the crow uses to search for an appropriate whelk, the energy in flying to the site where the rocks are, and the energy required to lift the whelk to a certain height and drop it times the number of vertical flights required to split open the whelk. We will concentrate only on the energy of this last component of the problem, as it was observed that the crows kept with the same whelk until they broke it open rather than searching for another whelk when one failed to break after a few attempts.

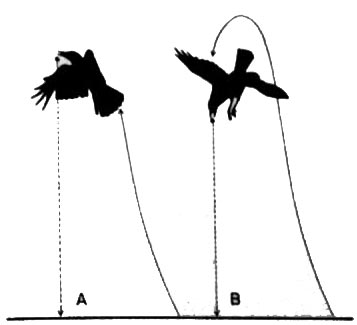
Thus, the energy that we measure is given by the height (H) times the number of drops (N) or

 where k is a constant of proportionality. Notice that flying higher and increasing the number of drops both increase the use of energy.

Data from Zach's research was used to find a function that expresses the number of drops (N) as a function of the height (H). Since it always requires at least one drop, the proposed function is

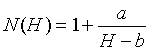
The graph below shows the least squares best fit of this function to Zach's data and gives a = 15.97 and b = 1.209.
 
 

Thus, the Energy function becomes

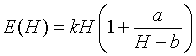
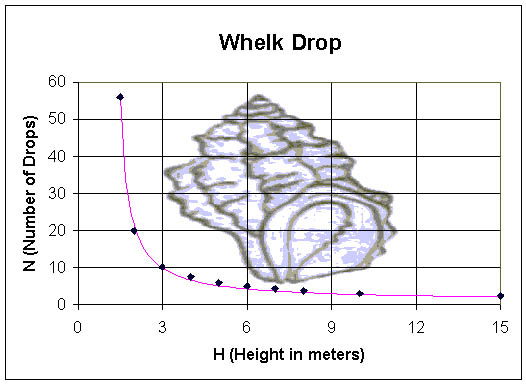
A graph of this function with the values of a and b above and k = 1 is shown below.
 
 

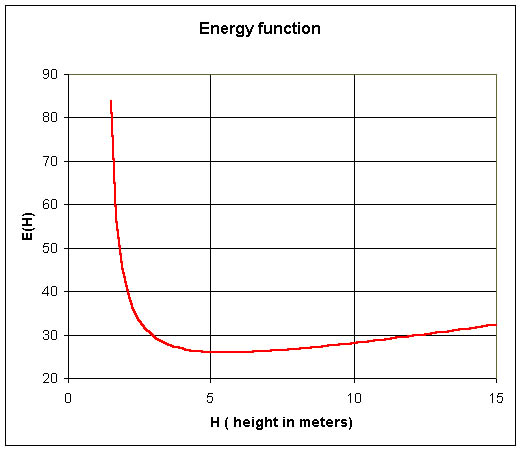
A minimum energy is readily apparent from the graph with the value around 5.6 m, which is close to the observed value that Zach found the crows to fly when dropping whelks.

To find the specific value from our formula, we take the derivative and set it equal to zero, solving for H. The derivative of the expression of E(H) uses the product rule and either the quotient rule or chain rule giving:

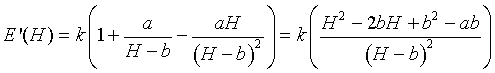
For the derivative to be zero, the numerator must be zero. But the numerator is just a quadratic equation. With the values of a and b above, the numerator is zero for  both H = 5.602 and H = -3.185. Obviously, the second answer doesn't make sense for this problem (it is a maximum of this function, and a negative height), so the minimum energy occurs at H = 5.602 m. This agrees with the graphical observation, and the experimental results.

Optimal Solution

One application of the derivative is to find critical points where often a function has a relative minimum or maximum. An optimal solution for a function is when the function takes on an absolute minimum or maximum over its domain.

Definition: An absolute minimum for a function f(x) occurs at a point x = c, if f(c) < f(x) for all x in the domain of f.

Theorem: Suppose that f(x) is a continuous, differential function on a closed interval I = [a, b], then f(x) achieves its absolute minimum (or maximum) on I and its minimum (or maximum) occurs either at a point where f '(x) = 0 or at one of the endpoints of the interval.

Optimal Study Area

An ecology student goes into the field with 120 m of string and wants to create two adjacent rectangular study areas with the maximum area possible. Below is a diagram of the two study plots.

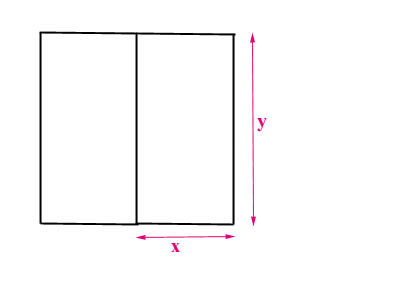
If each region has length y and width x, sharing one common length between, then from the diagram above it is clear that the amount of string needed to mark off the region is

The area of each rectangular plot is

Clearly, the optimal solution uses all the string, so P = 120. We can solve the first equation for y and obtain

Thus, area can be written as a function of x with

The domain of this function is 0 <x< 30, which is where the area is positive.

Differentiating A(x), we find

A critical point occurs when A'(x) = 0, so 40 - 8x/3 = 0 or x = 15. From the equation above for y, we see that the optimal y value is 20. Thus, to maximize the study areas, the ecology student should make each of the two study areas 15 m wide and 20 m long or 300 m².

There are more Worked Examples to provide additional information guiding your work on homework problems.

Chemical Reaction - Optimum at Endpoints

 One of the simplest chemical reactions is the combination of two substances to form a third. This reaction is written:

 

If the initial concentration of substance A is a and the initial concentration of B is b, then the law of mass action gives the following reaction rate for the bimolecular reaction:

where k is the rate constant of the reaction and x is the concentration of X during the reaction. What is the concentration of X where the reaction rate is at a maximum?

For graphing purposes, suppose that k = 50 (sec^-1), a = 6 (ppm), and b = 2 (ppm), so

From our theorem above, we seek critical points where the derivative is zero or the endpoints of the domain. The derivative equal to zero gives:

Note that this critical point is outside the domain (and produces a negative reaction rate). So we turn to examining the endpoints. Below is a graph of R(x). We see that the maximum rate is at the beginning of the reaction with no product X (R(0) = 600) and the minimum occurs at x = 2, where the reaction rate is zero.

References:

[1] R. Zach (1978) Selection and dropping of whelks by Northwestern crows, Behaviour, 67, 134 - 147
[2] R. Zach (1979) Shell dropping: Decision-Making and optimal foraging in Northwestern crows, Behavior, 68, 106 - 117