1. Differentiation of Trigonometric Functions
2. Extrema for a Damped Oscillator
3. Maximum Change in Temperature 

This section examines sample problems for differentiation of trigonometric functions. The examples include some basic differentiations, finding extrema, and an application of the derivative of the sine function to rates of change in temperature.

Example 1: Differentiation of Trigonometric Functions. Find the derivatives for the following functions:

Solution: We begin with f(x), which uses the product rule and the chain rule. It follows that

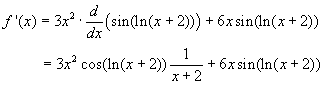
This used the fact that d(ln(x+2))/dx = 1/(x+2).

For g(x), we only need to apply the chain rule. Thus,

This used the fact that d(-cos(2x+1))/dx = 2 sin(2x+1).

Example 2: Extrema for a Damped Oscillator. Consider the function

which describes the motion of a damped oscillator, like shock absorbers on a car. Find the absolute maximum and minimum for this function for t > 0. Sketch a graph of this function.

Solution: We begin this problem by finding the derivative of f(t). Applying the product rule, we find that

The extrema occur when f '(t) = 0, which happens whenever cos(t) = sin(t). From the previous section, we know that sine and cosine are equal at p/4 radians, then again at 5p/4 radians and every p radians afterwards. The exponential function damps this solution to zero (a horizontal asymptote of y = 0), so the largest positive and negative values will occur at the first relative maximum and minimum, which are

Below we see a graph of this function for 0 < t < 5.

Example 3: Maximum Change in Temperature. Often the sine function is used to approximate the temperature during a day. Suppose that the coolest temperature for a day occurs at 3 am and is 56^oF. If twelve hours later, the hottest temperature of 82^oF occurs. Assume that the temperature, T(t) satisfies the following function:

where the constants A, B, w, and f are to be determined from the data. Find the constants that best best the data for the temperature during the day assuming that the temperature has a 24 hour period. Determine the times during the day that the temperature is rising most rapidly and falling most rapidly, and give the rate of change of temperature at those times.

Solution: From the data, we assume that the average temperature is given by

The amplitude of this function is found from the difference between the high temperature and the average temperature, so

We are assuming 24 hour periodicity, so 24w = 2p or w = p/12. The maximum of the sine function occurs at p/2, and we are assuming that the maximum temperature occurs at 3 pm or t = 15 hours. Thus, we find the phase shift f by solving

The last equation is readily solved by multiplying through by 12/p, giving

Thus, our temperature function is given by the formula:

The graph of this function is seen below.

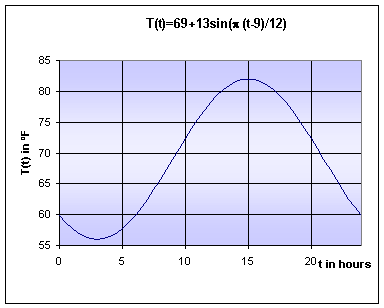
From the graph, it appears that the temperature is rising most rapidly in the morning, and it is falling most rapidly in the evening. The rate of change in temperature is given by the derivative of T(t), which satisfies

A graph of this function is seen below:

There are two ways to determine the maximum and minimum of this graph. The first is to use our knowledge about the cosine function and where its highest and lowest values are, and the second is to take the second derivative (or derivative of the derivative function) and determine when it is 0. Since we are practicing derivatives in this section, we will begin with the second method. The derivative T '(t) of is given by:

This is zero when sin(p(t - 9)/12) = 0 or the argument p(t - 9)/12 is some integer multiple of p. Thus, we need to solve

It is easy to see that the only solutions in the first 24 hours are t = 9 and 21. Notice that these times are when the cosine function is first 1 (the maximum increase) and then -1 (the maximum decrease). Substituting these values into the derivative function, T '(t), we find the maximum increase occurring at 9 am with

Similarly, the maximum decrease occurs at t = 21 or 9 PM, and is found by computing