Introduction

• Professor Short introduced Epidemic Models
• Mathematical models showed that a disease like malaria could be extinguished without destroying all mosquitoes
• Ecological significance is that below a critical number populations can go extinct
• We examine the population dynamics of a simple predator-prey system

• Hudson Bay company kept careful records of all furs from the early 1800s into the 1900s
• Assume that furs are representative of the populations in the wild because of the trapping intensity and trapping techniques
• Records of furs showed distinctive oscillations with a period of about 12 years for lynx and hares
• Lynx primarily eat snowshoe hares, which makes this a rare two species (simplified) interaction - (Mathematical models have a hard time understanding multiple species interactions)
• Ecologists have predicted that in a simple predator-prey system that a rise in prey population is followed (with a lag) by a rise in the predator population - when the predator population is sufficiently high, then the prey population begins dropping - thus, oscillations occur
• Can a mathematical model predict this?
• What causes cycles to slow or speed up? What affects the amplitude of the oscillation or do you expect to see the oscillations damp to a stable equilibrium?
• The models tend to ignore factors like climate and other complicating factors - how significant are these?

• Single species growth model with population P_n and growth function g(P_n) is given by

• Malthusian Growth model satisfies

• This equation is easily solved (recall compound interest problems)

• This gives exponential growth. Until recently and with a few exceptions like the plague years, human growth has been very consistently Malthusian.
• When the growth function g(P_n) is more complicated, then other mathematical techniques are needed. We will use computer simulations.

• Define the hare population by H_n and the lynx population by L_n
• Assume the primary growth of the hare population is Malthusian, a₁H_n, (in the absence of lynx) and that the lynx population, -b₁L_n, (in the absence of hares) is negative Malthusian
• Assume that the primary loss of hares is due to predation (contact) with lynx, -a₂H_nL_n, and that the growth of the lynx population is from energy derived from eating hares, b₂H_nL_n
• The Lotka-Volterra model is given by

Simulation of the Model

• Excel worksheet to be developed!

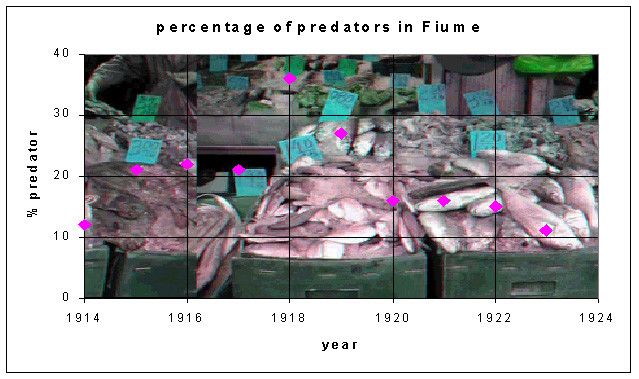
• Following World War I, Volterra examined the fishing data for Italy and discovered that the percent of sharks and skates in the fishing catch rose during the years of the war

 

Percentages of predators in the Fiume fish catch

1914	1915	1916	1917	1918	1919	1920	1921	1922	1923
12	21	22	21	36	27	16	16	15	11

• These data don't show oscillations, but there is clearly a rise and fall of the percent of sharks and skates in the fish catch due to effects of the war. What caused this?
• Volterra used the predator-prey model to show why this effect could be predicted
• Let F_n be the food fish population and S_n be the shark and skate population. To the Lotka-Volterra model, we add the effects of human fishing (using nets, -a₃F_n and - b₃S_n ), then the mathematical model becomes

Equilibria

• An equilibrium for a population is when the population stays the same for all time or for each value of n. For the previous model, we have

• It can be shown (mathematically) that the average population about a cycle of the Lotka-Volterra model is its equilibrium value. Thus, if the fishing populations are cycling less than annually, the annual catch should reflect the equilibrium population
• Substitute the equilibrium information into the equations above

• Apply some algebra. The first two terms of each equation cancel, then factor F_e from the first equation and S_e from the second equation. The result is

• The product of two factors being zero means one of the factors is zero. From the first equation

• From the second equation

• Simultaneously, solving the two equations, we have the two equilibria, either

Relating Equilibria to Fishing Data

• With NO fishing, the nonzero equilibrium is

• With fishing, the nonzero equilibrium is

• Notice that as the level of fishing increases (a₃ and b₃ increasing), the equilibrium value for the food fish increases, while the equilibrium for the sharks and skates decreases. During World War I, the fishing fleets would be less likely to go out. Thus, the level of fishing decreases, which aids the equilibrium for the sharks and skates as reflected in the data!

• Consider an agricultural situation, such as scale insects and lady bugs, and the application of pesticides.
• Without pesticides, the insects form a classical predator-prey situation as modeled above.
• The application of pesticides is like the situation above with the fishing industry netting fish. The pesticide generally kills both the prey insect (which is usually the agricultural pest) and the predator species.
• Our analysis above shows that the prey species in the long run benefits from this type of application. Thus, the agricultural pest actually does better after application of pesticides (after a recovery time). This process causes even larger amplitude oscillations, so nastier outbreaks.
• Conclusion: The farmers and public lose from pesticides, while the chemistry industry benefits!